Inscription / Connexion Nouveau Sujet
Allure de la fonction dérivée
Bonjour 
J'ai un exercice à faire pour lundi mais je n'arrive qu'à en faire la moitié. L'énoncé est le suivant :
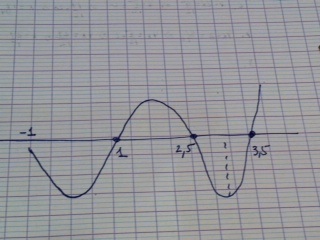
Soit f une fonction définie sur l'intervalle [-1 ; 5] donc la représentation graphique est donnée. Dans chaque cas, donner l'allure approximative de la courbe représentative de la fonction f', dérivée de la fonction f sur l'intervalle [-1 ; 5].
Pour la courbe a) c'est une fonction affine, j'ai trouvé l'équation de la fonction c'est à dire 0.5x - 1, j'ai dérivé il reste donc que 0.5. La courbe de f' est donc une droite d'équation y=0.5.
Pour le b) on a deux fonctions affines la première est croissante sur [-1 ; 1] son équation est x + 2, sa dérivée est 1. Sur [-1 ; 1] la courbe de f' est donc une droite d'équation y=1. Et sur [1 ; 5] l'équation de f est -x - 2, sa dérivée est -1. La courbe de f' sur [1 ; 5] est donc une droite d'équation y=-1.
Jusque là c'est assez simple mais après je n'y arrive pas du tout j'ai vraiment aucune piste 
Merci de votre aide

Salut!
Pour c), c'est une parabole (representation d'une fonction de seconde degré). Donc, sa dérivée est une ligne droite de coéfficient directeur positive (d'abord négative et après positive). La dérivée est égale à zéro près de x=1.
Pour d),ce sera un ensemble de droites croissantes et décroissantes selon les intervalles de croissance et décroissance de la fonction.
Johnny
Merci pour ta réponse
En fait je comprends que vers le point x=1 la dérivée sera égale à 0 mais je ne comprends pas comment trouver le coeff directeur de cette dérivée
Impossible de le determiner de façon exacte. Le graphique de laparabole ne donne aucun point dont les coordonnées soient faciles à reperer. Cependant tu peux calculer une équation aproximée.
Une fonctio de seconde degrée est de la forme
f(x) = a(x-x1)(x-x2)
où x1, x2 sont ses racines.
Comme x1 et x2 tu prendra -1 et 2 (approximées)
f(x) = a(x+1)(x-2)
Pour calculer a tu peux utiliser le point sommet P (plus ou moins) de coordonnées approximatives P(1/2; -3)
Après il ne reste qu'à developper et dériver.
Johnny
Ok donc :
y = a(x+1)(x-2)
-3 = a(1/2+1)(1/2-2)
-3/(1/2+1)(1/2-2) = a
a = 1.3
f(x) = 1.3x²-1.3x-2.6
f'(x) = 2.6x-1.3
On a bien f(0.5)=0 ce qui correspond à la courbe donnée par Barney
pour le d) on va avoir une succession de droites comme au b) ? parce que ça me semble bizarre vu que les deux courbes ne se ressemblent pas du tout
Sur [-1 ; 1] la fonction est décroissante, la dérivée sera négative.