Bonjour,

Le début de ton énoncé est incohérent : tu parles d'une triangle équilatéral AOI et ensuite tu dis que (on s'attendait plutôt à )
D'après ta figure (très approximative), ce ne serait pas plutôt ?

Euh oui en effet je me suis trompé donc je récapitule :

Salut à tous , j'ai un petit problème au niveau de cette énoncé que voici ; En effet , je n'arrive pas à résoudre ces questions et je doute sur les réponses auquels je vous les donne :

(Légende : *: Vecteur )
Soit un triangle équilatéral AOI tel que (*AO,*AI)=pie/3 (60degres)
les triangles OIJ ET IBA sont rectaangles isoceles tels que (*OI,*OJ)=(*IB,*IA)=pie/2

1)Faire une figure que voici :

[URL=http://website.hu][/URL]

quelle est la nature du triangle AOJ ? => Triangle Aoj Isocele.

2a) Démontrer que (*AJ,*AO)=5pie/12. (calculer d'abord AOJ ) ( IOJ = 90degres et AOI = 60  donc AOJ = 150)

b) Justifier l'égalité de (*AO,*AI) et de (*AI,*AB), en justifiant.

c) justifier l'égalité (*AJ,*AB) = (*AJ+*AO)+(*AO,*AI)+(*AI,*AB)

3
a) Calculer alors une mesure de (*AJ,*AB), en utilisant le 2)
b) que pouvez vous en deduire pour les points A,B,J ?

Merci infiniment pour les réponses attendus merci et je vous souhaite une agréable soirée , au plaisir merci .

Je suis d'accord avec toi :  AOJ est bien un triangle isocèle car OA=OI puis OI=OJ d'où OA=OJ
Par contre, je ne suis pas d'accord sur la mesure de l'angle . Pour moi cet angle vaut .

J'ai refait ta figure... Est-ce bien cela ?

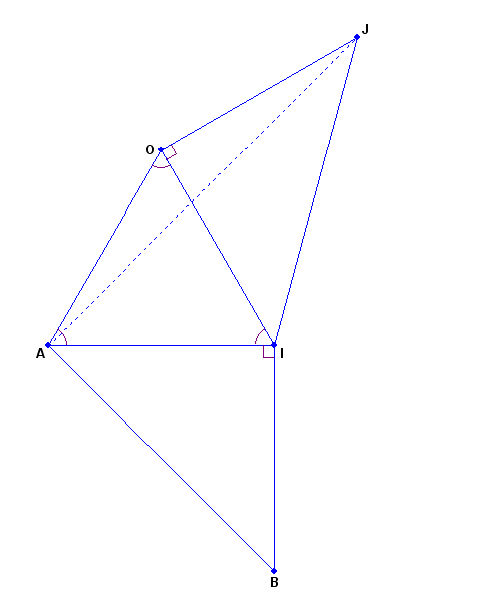
oui exactement , préssé par le temp , j'ai fait approximativement la figure sur paint...
oui à moi aussi , cela me parait louche que (*AJ,*AO)=5pie/12
mais c'est  selon la consigne , soit c'est la figure que j'ai fait qui est eronnée ou bien c'est lexo...

Je crois en effet, que tu as mal lu l'énoncé. D'ailleurs, si et non pas , l

zut, le coup est parti tout seul

... et non pas ,  la figure est plutôt celle ci-dessous. Si tu avaiscopié correctement ton énoncé, on n'aurait pas perdu tout ce temps !

Je rectifié tout ça

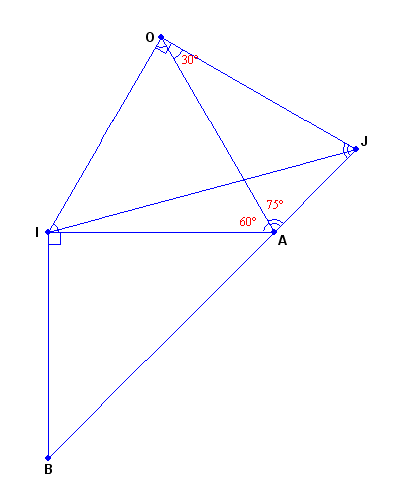
oui mais cependant il y'a quelquechose qui me turlepine dans ton énoncé , le sens de (*AI,*Ao) = - pie/3 ?.

Sachant que le sens d'un angle oriénté est positive ( sens inverse aiguille d'une montre)  et négative ( sens aiguille d'une montre).

Dans ton énoncé du 18/02/2008 à 18:56, tu parles bien de ...Il faut dire que ton énoncé est ... à géométrie variable

PS La lettre , si tu ne veux pas utiliser les symboles, s'écrit "pi" et non pas "pie" (tu dois confondre avec l'oiseau)

sachant que le triangle IOA étant un triangle équilatéral donc tout ces angles équivalent à 60degres , on a pour l'angle  AOJ partagé et donc 30degres ce que tu démontres sur ta figure est cela ?

mais alors comment pourrait-t-on démontrer que (*AI,*AO)=5pie/12 ?
c'est ce truc que je comprend pas

Il est impossible de démontrer que car puisque c'est l'un des angles du triangle équilatéral direct AOI. Encore une fois ton énoncé est incompréhensible !

En revanche, dans le triangle isocèle OAJ, l'angle au sommet O vaut 30° (/6) donc les 2 angles égaux de la base valent en tout 5/6 (150°), donc chacun d'eux vaut la moitié, c'est à dire 5/12 (75°) ...

donc c'est ce que j'avais anoncé pour la 1 , pour le message posté le 18/02/2008 à 19:56 sauf que j'avais fait tt à l'envers , en bref

pour ces questions :
b) Justifier l'égalité de (*AO,*AI) et de (*AI,*AB), en justifiant.

c) justifier l'égalité (*AJ,*AB) = (*AJ+*AO)+(*AO,*AI)+(*AI,*AB)

3
a) Calculer alors une mesure de (*AJ,*AB), en utilisant le 2)
b) que pouvez vous en deduire pour les points A,B,J ?

il faut utiliser l'expression analytique ?

b) car AOI est un triangle équilatéral direct,
car AIB est isocèle rectangle direct en I.

c) l'égalité est vraie quels que soient les angles : c'est la relation de Chasles qyui s'applique.

3)a) pour , ça donne
b) on en déduit que les points A,B,J sont alignés (angle de 180°). Il n'est nul besoin de recourir à l'expression analytique.