Inscription / Connexion Nouveau Sujet
angles orientés 2 triangle
Bonjour  ,
,
Voici un exercice : ABC est un triangle équilatéral tel que : (BC,BA) =
AHE est un triangle rectangle isocèle tel que (HA,HE) =
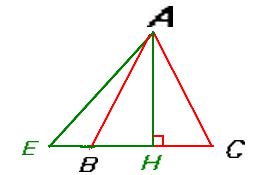
(Voir figure ci-dessous)
Trouvez la mesure principale des angles :
a) (AC,AE) Je n'ai pas réussi à faire celui -ci 
b) (BA,CB)
c) (AH,EB)
d) (EA,CH)
Les 2 vecteurs ont effectivement même direction , mais pas même sens , c'est pourquoi l'angle (HE,EB) a une mesure égale à 
Bonjour, j'ai cet exercice pour la rentrée et je n'y comprend strictement rien... Je voudrais savoir si quelqu'un pourrait me dire comment on fait pour la question D svp
Bonsoir Totoche77,
(EA,CH) = (EA,HA) + (HA,CH) ( propriété citée le 02-01-12 à 14:16 )
Or (EA,HA) = (AE,AH) =  /4 car AHE est un triangle rectangle isocèle
/4 car AHE est un triangle rectangle isocèle
et
(HA,CH) = (HA,HC) +  = -
= - /2 +
/2 +  =
=  /2
/2
Donc (EA,CH) =  /4 +
/4 +  /2 = 3
/2 = 3 /4
/4
Merci pour cette réponse! 
Je voulais savoir si pour la a) on peut mettre :
(AC, AE) = ((AB,Ac)/2)+(AE, AH)
(AC, AE) = (- /3)/2 - (
/3)/2 - ( /4)
/4)
(AC, AE) = ( - /6) - (
/6) - ( /4) = -(5
/4) = -(5 /12)
/12)
Ta réponse est correcte , mais attention (AB,AC) = +  /3 et (AE,AH)= +
/3 et (AE,AH)= +  /4
/4
On peut mettre (AC,AE) = (AC,AH) + (AH,AE) = - /6 + (-
/6 + (- /4) = -5/12
/4) = -5/12


