Inscription / Connexion Nouveau Sujet
angles orientés
Bonjour,
je suis bloquée à partir de la question 4
Alors si quelqu'un pouvait m'orienter (on relèvera le jeu de mots ^^)...
Voila l'énoncé :
"On considère un triangle ABC direct, isocèle et rectangle en A. On construit les deux triangles équilatéraux indirects AIC et BJA.
Le but de cet exercice est de démontrer que les droites (IJ) et (BC) sont parallèles.
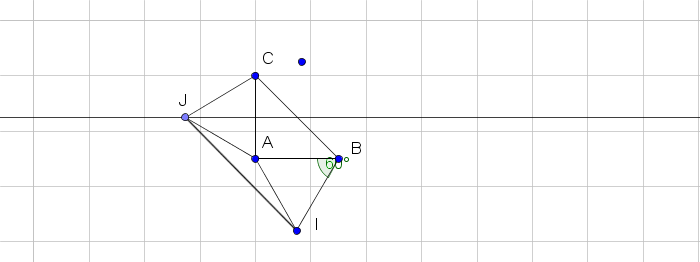
1/ Faire la figure
2/ a- déterminer la mesure de chacun des angles orientés suivants :
(AB;AC) (AJ;AB) (AC;AI) (il manque les flèches au dessus des vecteurs)
b- en déduire une mesure de l'angle orienté (AJ;AI)
3/ a- determiner la nature du triangle AJI
b- En déduire une mesure de l'angle orienté (JI;JA)
4/ determiner une mesure de chacun des angles orientés suivants:
(JA;JB) (JB;BA) (BA;BC)
5/ déduire des questions 3/ et 4/ une mesure de l'angle orienté (JI;BC).
6/ conclure."
Voila, je suis donc bloqué au 1° angle orienté de la question 4/.
Merci pour votre aide.
bonjour,
4/ determiner une mesure de chacun des angles orientés suivants:
(JA;JB) (JB;BA) (BA;BC)
(JA;JB) : c'est là que tu es bloqué?
on te dit :
On construit les deux triangles équilatéraux indirects AIC et BJA.
sans indiscrétion, peux-tu nous poster tes réponses :
2/ a- déterminer la mesure de chacun des angles orientés suivants :
(AB;AC) =...... (AJ;AB)=....... (AC;AI)=........
b- en déduire une mesure de l'angle orienté (AJ;AI)=.......................................
3/ a- determiner la nature du triangle AJI:........................................................
b- En déduire une mesure de l'angle orienté (JI;JA)
Pour la 2) a) j'ai
(AB;AC)=pi/2 (modulo 2pi)
(AJ;AB) =PI/3 (modulo 2pi)
(AC;AI)= PI/3 (modulo 2pi)
2)b) (AJ;AI)= pi/3 mais je pense que je me suis trompée car ça ne colle pas avec le dessin.
3)a) AJI est un triangle isocèle en A car AI=AJ
b) (JI;JA)= je ne trouve pas
4) 5) 6) je n'y arrive pas !
2)b) (AJ;AI)= pi/3 mais je pense que je me suis trompée car ça ne colle pas avec le dessin.
chasles:
(AJ;AI)= (AJ;AB)+(AB;AC)+(AC;AI)
C'est exactement ce que j'ai fait : (AJ;AI)= (AJ;AB)+(AB;AC)+(AC;AI)
= pi/3 +pi/2+pi/3 = 7pi/3 (modulo 2PI)= pi/3
Je viens de comprendre : cen'est pas 7pi/3 mais 7pi/6 !! Donc au final la mesure principale est -5pi/6 !!
Pouvez-vous m'aider pour la suite:
pour (JI,JA) je trouve pi/12
et la suite je ne vois pas comment faire
ça j'y suis arrivée mais c'est la suite
pour (JI,JA) je trouve pi/12
et la suite je ne vois pas comment faire