Bonsoir,
Pense qu'il est plus simple de lire un angle de vecteurs quand ils ont meme origine

Trace par exemple le vecteur AB'egal au vecteur CB

Salut

Pour te représenter l'angle orienté (vec AB, vec CB), tu dois les faire partir du même point d'application

D'ailleurs tu peux remarquer que  

Ensuite comme on mesure les angles dans le sens trigonométrique, c'est à dire antihoraire, la vraie mesure est -60° ou -pi/3 rad, car l'angle ABC est dans le sens horaire donc il faut en prendre l'opposé

Mais vu que tu es censé les lire graphiquement, tu n'as qu'à déplacer dans ta tête le vecteur CB en le faisant partir du point A, et tu vois que l'angle (AB,CB) est -pi/3

bonjour,

"pour mieux voir" il est conseillé de prendre un vecteur égal à CB, de même origine que AB



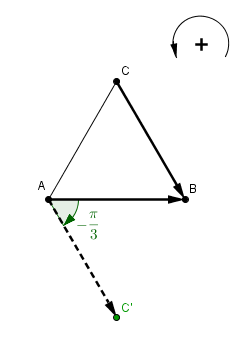
sinon sens direct cela veut dire que {vAB; vAC) = + pi/3
et que par permutation circulaire {vBC; vBA) = + pi/3 et {vCA; vCB) = + pi/3

Attention Zormuche , la mesure de ton angle de vecteurs est fausse : ce n'est pas l'angle géométrique

Merci beaucoup , je comprends maintenant mon erreur, j'ai pris comme même origine B et non A
Merci à tous pour vos réponses aussi rapides !!!

si on veut le faire "propre" (c'est à dire pas en observant graphiquement)
on part de (vBC; vBA) = + pi/3 (définition de triangle direct)
et on applique des règles de calcul saines c'est à dire explicitement Chasles, (v; -v) = pi et (u; v) = -(v; u) sans plus rien regarder de la figure.
en faisant les calculs "modulo 2pi" (c'est à dire à 2pi près)

(vAB, vCB) = (vAB, vBA) + (vBA, vBC) + (vBC, vCB) (Chasles)
= pi + (vBA, vBC) + pi modulo 2pi
= (vBA, vBC) modulo 2pi (pi + pi = 2pi = 0 modulo 2pi)
= -(vBC; vBA) = -pi/3 modulo 2pi

Bonsoir Mathafou : ce qui est la methode la plus rigoureuse!

on a aussi le droit de prendre quelques raccourcis l'habitude venant : (u; v) = (-u; -v)
(c'est mes trois premières lignes)