Inscription / Connexion Nouveau Sujet
Approximation affine d'une fonction au voisinage de a.
Salut à tous ! 
Alors voila problème avec les dérivation !
D'après la définition d'un nombre dérivé, quand une fonction f es dérivable en a, on a :
f'(a) = lim(h 
0) (f(a+h) - f(a) )/h
On montre que l'égalité précédente est équivalente à l'égalité suivante :
(f(a+h) - f(a) )/h = f' (a) + 
(h) avec lim h0 = 0
1) Démontrer l'égalité :
f(a+h) = f'(a) + f'(a)h + h(h)
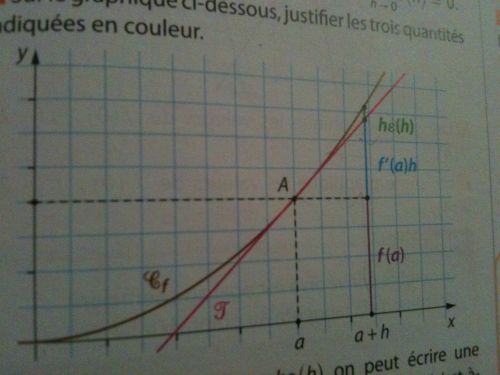
2) Sur le graphique ci-dessous, justifier les trois quantités indiquées en couleur. (je vous joint l'image ci-dessous)
3) Si on néglige le terme h(h) on peut écrire une approximation de f(a+h) au voisinage de a ( c'est-a-dire pour h proche de 0) sous la forme :
f(a+h) 
f(a) + f'(a)h
On dit que h f(a) + f'(a)h est une approximation affine de f(a+h) lorsque h est proche de 0.
Justifier l'appellation "approximation affine".
4) a. Ecrire cette approximation affine lorsque f est la fonction racine carrée et pour a =1.
b. Application numérique : trouver, sans calculatrice une valeur approchée des réels suivant : 
1.02 et 0.996
_____________________________________________________________________________________________________
_____________________________________________________________________________________________________
1) (f(a+h) - f(a) )/h = f' (a) + (h)
(f(a+h) - f(a) ) = f' (a)h + h(h)
f(a+h) = f(a) + f'(a) h+ h (h)
2) La quantité de la couleur violette correspond à l'ordonné du point A
Pour, le bleu et le vert, je ne vois pas ! 
3) Je ne comprend pas du tout à partir de là !
Merci d'avance pour vos aide 
bonjour
je viens essayer de t'expliquer sans dire trop de bêtises... en espérant que l'on me reprendra si c'est le cas.
en rouge, tu as la tangente en a; le segment bleu est égal au coeff. directeur de la tangente multiplié par h; il correspond donc à la variation d'ordonnée selon la valeur de h
par rapport à 'a', on avance de h, et on 'monte' de f '(a)h --> le rapport f '(a)h / h = f '(a) = coeff directeur de la tangente
plus h est choisi petit, plus f '(a)h tendra vers 0
le segment vert correspond à la distance entre la tangente et la courbe; là encore, plus h est petit, plus cette quantité epsilon sera faible, et plus l'approximation affine sera fiable.
3) une fonction affine est de la forme ax+b... tu vas trouver 
4) f(x) = x
f '(x) = 1/(2x)
donc l'approximation affine à proximité de a est :
g(h) = f(a) + f'(a)h = h/(2a) + a
1.02 --> pose a = 1 et h = 0.02
que trouves-tu ?
2) Je pense avoir compris ! Merci pour tes explications
3) Il s'agit d'une fonction affine en fonction de la variable h ?
4) h -> Vh - 1/ 2Vx
Enfaîte, ça je ne comprend pas :s
En tout cas, merci pour ta réponse ( et désolé si j'ai mis du temps à répondre) 
3) ok
4) On dit que h --> f(a) + f'(a)h est une approximation affine de f(a+h) lorsque h est proche de 0.
Ecrire cette approximation affine lorsque f est la fonction racine carrée et pour a =1.
ici f(x) = x
donc f '(x) = 1/(2x)
et a = 1
donc l'approximation affine au voisinage de 1 est la fonction
h --> f(1) + f'(1)h, soit (1/2)h + 1
ainsi pour calculer par exemple 1.02
on pose a = 1 et h = 0.02 <---- donc a+h = 1.02
en utilisant l'approximation affine précédente on a 1.02 (1/2)*0.02 + 1 = 1.01
alors qu'à la calculette, on afficherait : 1.00995.... donc précision ici à 10-4 près.
bonne soirée
Annuler
connectez vous