Inscription / Connexion Nouveau Sujet
Approximer le nombre pi
Bonjour, j'ai un exercice sur la trigonométrie et sur l'approximation du nombre pi en utilisant la méthode d'Archimède. Cependant j'ai du mal avec cet exercice c'est pour ça que je suis là. Je suis arrivé à la question suivante :
Combien mesure l'angle HOA ? Expliquer brièvement ( sur la figure )
Merci pour votre aide !
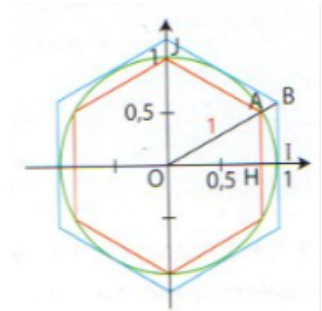
J'ai un autre petit problème dans les questions d'après.
On note u et v les demi périmètres des polygones à n côtés respectivement inscrit et
circonscrit au cercle de rayon 1.
Archimède a démontré que :
-le demi périmètre du polygone à 2n côtés circonscrit au cercle est : y = ( 2uv ) / (u + v )
- le demi périmètre du polygone à 2n côtés inscrit dans le cercle est : √uy
Je ne comprend pas ce qu'est y dans les formules et aussi je ne comprend pas pourquoi c'est 2n côtés
Merci pour votre aide
c'est 2n côtés parce que c'est facile de diviser un angle par 2, donc de doubler le nombre de côtés, (sinon les formules données en dessous seraient bien plus compliquées)
y est défini comme étant je cite : "le demi périmètre du polygone à 2n côtés circonscrit au cercle" !!
et il se calcule à partir de u et v qui sont définis comme étant je cite encore :
"u et v les demi périmètres des polygones à n côtés respectivement inscrit et
circonscrit au cercle de rayon 1"
en utilisant la formule indiquée.
et dans la deuxième formule on utilise cette valeur de y pour calculer "le demi périmètre du polygone à 2n côtés inscrit dans le cercle"


