Inscription / Connexion Nouveau Sujet
Asymptote
Bonjour.
Je suis en train de faire un exercice et je bloque déjà sur la première question.
Soit f une fonction définie sur R* par f(x)= (-x²+x+1)/x
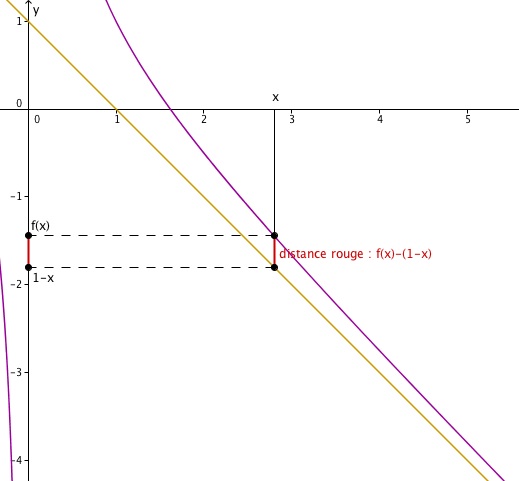
Il faut que je prouve qu'il y a une asymptote 
d'équation y=1-x
J'ai donc fait, (mais je ne suis pas sure):
f(x)-(1-x) ce que me donne 1/x.
Mais après ?
Merci d'avance !
(Je suis nouvelle sur ce forum, j'espère avoir bien respecté les règles.)
Bonjour,
Pour l'instant c'est bon.
Graphiquement, f(x)-(1-x) c'est la différence de hauteur, à l'abscisse x, entre le point de la courbe Cf et le point de la droite ∆. Tu le vois ?
Pour montrer que ∆ est asymptote à Cf (en ±infini), tu dois montrer que cette différence tend vers 0 quand x tend vers l'infini (graphiquement, ça signifie que la courbe se rapproche de la droite jusqu'à presque la toucher).
Et bienvenue 
!
Annuler
connectez vous