Inscription / Connexion Nouveau Sujet
Barycentre
Bon voila, j' ai quelques difficultés sur un exercice concernant le chapitre " Barycentre ", dont voici l' énoncé :
On considère un triangle ABC du plan.
1) a° Déterminer et construire le point G, barycentre de
[(A;1);(B;-1);(C;1)].
b° Déterminer et construire le point G', barycentre de
[(A;1);(B;5);(C;-2)].
2) a° Soit J le milieu de [AB].
Exprimer ' et
' en fonction de
et
et en déduire l' intersection des droites (GG') et (AB).
b° Montrer que le barycentre I de [(B;2);(C;-1)] appartient à (GG').
c° Soit D un point quelconque du plan. Soient O le milieu de [CD] et K le milieu de [OA].
3) Déterminer trois réels a, d et c tels que K soit le barycentre de [(A;a);(D;d);(C;c)].
4) Soit X le point d' intersection de (DK) et (AC).
Déterminer les réels a' et c' tels que X soit barycentre de [(A;a');(C;c')].
*Pour la 1)a) j' obtiens:
=
*Pour la 1)b) j' obtiens :
' =
+
*Pour la 2)a) j' obtiens:
=
= - -
et
=
+
= - +
Mais lorqu' on me demade de déduire l' intersection des droites (GG') et ( AB) je suis bloqué.
Pouvez-vous m' aider s' il vous plaît, je vous en serai très reconnaissant, merci d' avance.
Oui, tu avais belle est bien raison, j' ai refait tous mes calculs et j' obtiens le même résultat que toi 
. Maintenant je n' ai plus qu' à tenter a suite. Je reviens en cas de problème, je te remercie encore cailloux
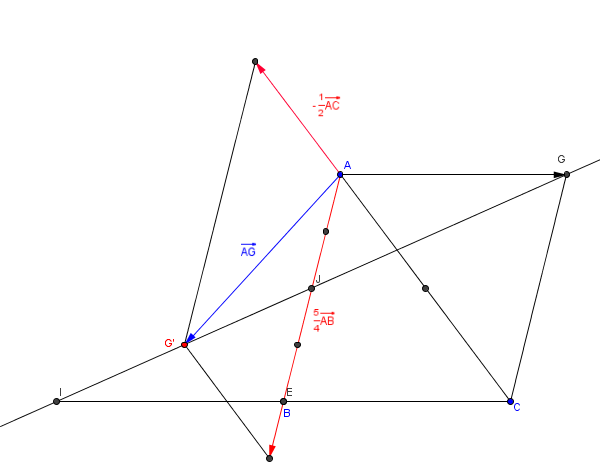
Par contre d' après mon schéma, G, J et G' ne sont pas alignés...
Cette figure est approximative mais c' est ce que j' obtiens un peu près.
Bonjour,
G' est mal placé...
Je vais te faire un petit dessin...Quelques minutes..
Pourquoi ton triangle (ABC je suppose) est- il rectangle ?
J' ai réussi la question 2)b) avec I= Bar[(G;1);(G';4)]
, mais je suis de nouveau bloqué à la question 3) 
Bonsoir,
est le milieu de
donc
barycentre de
et est le milieu de
donc
barycentre de
Par associativité des barycentres: barycentre de
Bonsoir
Pourquoi as-tu K=Bar[(A;2);(0;2)] ? Je pensais que tu devais obbtenir:
k=Bar[(A;1);(0;1)], même si c' est égual.
C' est pareil, mais pour utiliser l' associativité, il faut que les coefficients correspondent:
Je fais un raisonnement un peu différent:
Soit le barycentre de
est donc le barycentre de
par associativité, donc G est le milieu de
et
Ca te convient peut-être mieux, mais c' est la même chose...
Si j' étais parti de (A,1), j' aurais dit K milieu de [AO] est barycentre de
Mais O milieu de [CD] est barycentre de ; oui, mais avec l' associativité, je me retrouve avec un (O,2) au lieu d' avoir (O,1)
Je dois donc dire, pour avoir un cohérence dans les coefficients:
O barycentre de : moche.
J' ai pris le parti de doubler les coefficients en partant de (A,2)
D' ailleurs, pour mieux comprendre, trace un triangle ACD et construit le barycentre K avec les coefficients 2,1,1.
C'est bon "cailloux" j' ai tout compris , merci beacoup pour ton aide , j' essayes la suite demain .
Bonne soirée
Annuler
connectez vous