Inscription / Connexion Nouveau Sujet
Barycentre d'une plaque circulaire...
Bonjour! J'ai un DM a faire pendant ces vacances et cet exercice me pose un peu problème! On l'avais deja fait mais j'ai complètement oublié et je trouve plus la méthode... enfin bon voila l'exercice:
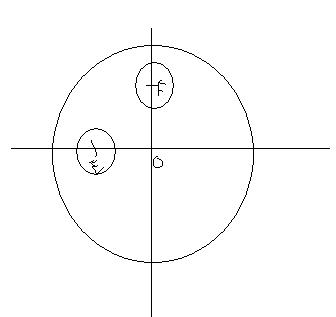
Une plaque métallique homogène circulaire est percée de deux petits disques, dont les centres sont les milieux de [OA] et [OB], les rayons étant tous de deux égaux à (OA)/4
1) construire le barycentre G de cette plaque.
dans le dessin O est le centre du cercle normalement.. et E et F le centre des 2 'trous'.
Merci pour votre aide!
Bonjour!! désolé je veux bien t'aider mais je ne comprend pas comment on peut faire pour trouver le barycentre d'une plaque!! j'ai déjà du mal avec un barycentr de 3 point pondérés et je n'ai pas commencé le barycentre de n point pondérés. Je suis vraiment désolée
 j'éspere que des gens pourront trouver une solution a ton problème. BONNE ANNEE a bientot
j'éspere que des gens pourront trouver une solution a ton problème. BONNE ANNEE a bientot
C'est deja une réponse... 
Bonne année à toi aussi!
J'ai une idée qui m'est venue mais je sais pas vraiment si ca va marcher....
Je me suis dit que l'aire de la grande plaque était l'aire d'un disque de même diamètre, moins l'aire des deux petits disques...
Après quoi j'ai essayé d'introduire le barycentre, et j'ai mit l'air du grand disque comme poids pondérée... ca donne ca ^o)...
A= 7 OA²/8
OA²/8
et Quant aux aires des petits disques il est de  OA²/16
OA²/16
Soit x bar. De (F;  OA²/16) et (E;
OA²/16) et (E;  OA²/16).
OA²/16).
G barycentre de (O; 14 OA²/16) (F;
OA²/16) (F;  OA²/16) et (E;
OA²/16) et (E;  OA²/16).
OA²/16).
Daprès le théorème du bar. partiel, G bar. (O; 14 OA²/16) et (x; 2
OA²/16) et (x; 2 OA²/16).
OA²/16).
On a alors
14 OA²/16) OG + xG 2
OA²/16) OG + xG 2 OA²/16 = 0 (OG, xG et O étant des vecteurs...)
OA²/16 = 0 (OG, xG et O étant des vecteurs...)
<=> ( OA²)OG + (2
OA²)OG + (2 OA²/16]xO = 0
OA²/16]xO = 0
mais je sais pas si c'est bon et je sais pas non plus quoi faire après... svp un peu d'aide!
wouaw tu m'épate!! ça a l'air bien vu que tu as trouver un barycentre mais après je n'ai pas encore vu le théoreme du barycentre partiel!! je suis vraiment désolée j'aurais voulu t'aider!! si c'était un truc facile de construction je t'aurais dit: pour construire un barycentre il faut utilisé l'égalité: par exemple g barycentre de ( A;1) et (B;2) alors vecteurAG=1/3 vecteurAB ( en fait c'est beta sur beta + alpha vecteurAB) mais bon si c'était facile tu aurais pu le trouvee tout(e) seul(e)!! a+
je suis vraiment désolée j'aurais voulu t'aider!! si c'était un truc facile de construction je t'aurais dit: pour construire un barycentre il faut utilisé l'égalité: par exemple g barycentre de ( A;1) et (B;2) alors vecteurAG=1/3 vecteurAB ( en fait c'est beta sur beta + alpha vecteurAB) mais bon si c'était facile tu aurais pu le trouvee tout(e) seul(e)!! a+
lol nan mais je sais pas vraiment si c'est bon donc bon...
A croire qu'il n'y a que nous sur ce forum XD
Pfiou quel casse tête :s

 ouais tout a fait d'accord avec toi!! la premiere s de toute façon c'est dur!! je suis désole ( encore une fois) de ne pas pouvoir t'aider je ne suis pas très forte pour les barycentre et les redoublants de ma classe non plus: à croire qu'il n'y a que les profs qui réussissent!!
ouais tout a fait d'accord avec toi!! la premiere s de toute façon c'est dur!! je suis désole ( encore une fois) de ne pas pouvoir t'aider je ne suis pas très forte pour les barycentre et les redoublants de ma classe non plus: à croire qu'il n'y a que les profs qui réussissent!!
a+ 
Lol nan cava mais ce qui complique tout c'est les petits trous qu'on y a percé sur cette plaque!
L'île est vraiment déserte aujourd'hui..... OO!
lol!! 2 déserteurs sur une ile ou les maths sont exigé!! faut croire que les autres ont été sauvé: retour vers la civilisation. on n'est quand meme pas les seuls!! il y a 530 visiteurs et je ne vais pas croire qu'il n'y en a pas un de 16 ou 17 ans qui ne puisse pas te répondre!!
bah lundi... XD
je sais je m'y prends tard, mais jai cherché tout seul et bon.. Dernier recours cétait l'île!!
Comme tu dis, 530 visiteurs et aucun ne vole à notre secours XD!
L'île déserte... wow quelle aventure XD
un demi millier de visiteur et personne pour m'aider... vraiment XD
théorème du barycentre partiel : G est le barycentre du système {(A, alpha); (B, beta); (C, gamma)}.
Supposons que \alpha + \beta \neq 0 et notons H le barycentre de {(A, alpha); (B, beta)}.
Alors G est le barycentre de {(H, alpha + beta); (C, gamma)} c'est bien ça que tu as utilisé? ( je l'ai trouvé sur le site) c'est bizarre mais ça me dit quelque chose!!par hasard c'est pas un synonyme de l'associativité du barycentre? parce que je suis devant mon cours et c'est exactement pareil!!
si AO et BO sont des rayons : une idée que j'ai comme ça mais je n sais pas si ça va fonctionner: alors: si tu fait G barycentre des points E et F et que tu le trace ça va peut-etr fonctionner. reste a trouver les coefficients ( ils auraient pu laisser la plaque sans trous quand même!!)
ah ou alors tu fais G barycentre de E ; F et O ce qui revient à faire ce que tu as fais!! bah alors c'est juste ton truc non?
de E ; F et O ce qui revient à faire ce que tu as fais!! bah alors c'est juste ton truc non?
bah c'est ce que jai fait en fait avec les barycentres et tout;
en fait j'ai fait le barycentre des deux petits cercles de centre E et F et de même rayon (OA/4)
puis grâce au théorème du barycentre partiel, j'ai fait le barycentre de G et de X (Xétant ce barycentre...)
Puis j'ai tracé, masi je suis pas sûr que ce soit ca!
Ca se trouve c'est ca ; le truc c'est tout bête et donc les gens i prennent pas la peine de répondre mdr XD
 tout bête!! moi j'ai pris la peine d'y répondre! mdr en tout cas je ne t'ai pas été d'une grand utilité vu que t'as réussi seul.
tout bête!! moi j'ai pris la peine d'y répondre! mdr en tout cas je ne t'ai pas été d'une grand utilité vu que t'as réussi seul.
c'est bien, quand je pense que moi j'ai un DM plus simple et que je bloque sur ds questions simples!!


