Inscription / Connexion Nouveau Sujet
Barycentre dans un triangle .
Bonsoir à vous , veuillez m'aider.
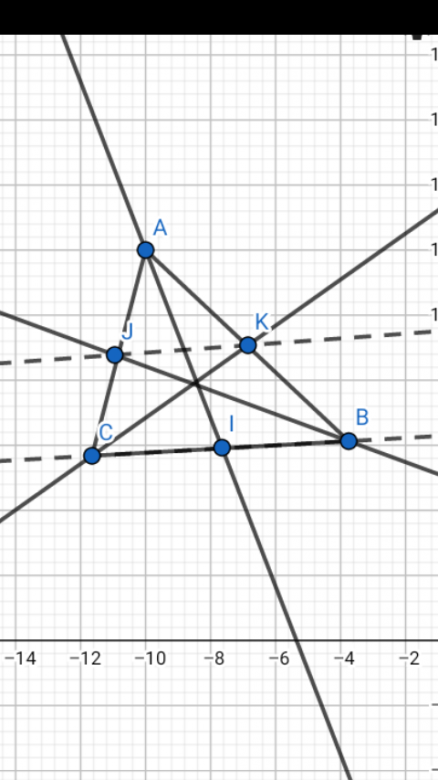
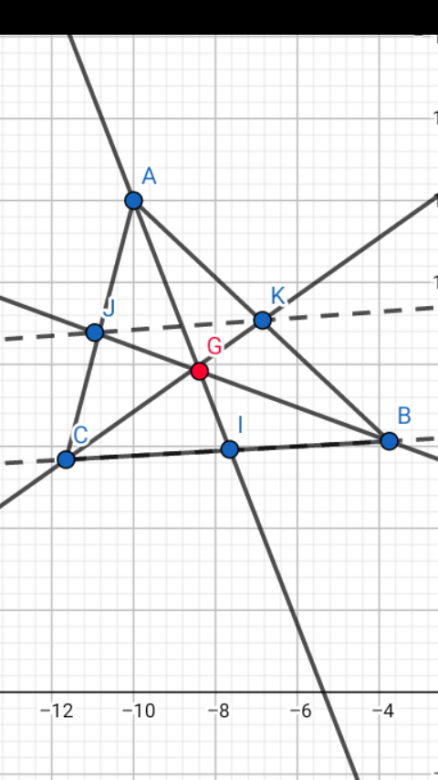
Soit ABC un triangle , p et q deux nombres réels positifs non nuls .On désigne par G le barycentre de (A,p) , (B,q) et
(C, q). Les droites (AG) , (BG) et (CG) coupent respectivement (BC) , (CA) et (AB) en I, J et K .
En utilisant le théorème des barycentres partiels , démontrer que :
a) I est le milieu [BC].
b) Les droites (JK) et (BC) sont parallèles .
Merci d'avance.
1/
G bary A(p) I(i) et I bary B(q) C(c)
d'où G bary A(p) B(q) C(c)
Or par hypothèse G bary de A(p) B(q) C(q)
On en déduit la valeur du coefficient c
Bonjour,
tu penses que ta réponse à un quelconque rapport avec la discussion en l'état et ce que demandait / disait pgeod ??
et pourquoi donc la mettre de façon aussi illisible (les tableaux de l'ile sont illisibles, en plus d'être difficile à saisir)...
tu penses que ta réponse à un quelconque rapport avec la discussion en l'état et ce que demandait / disait pgeod ??: peut être .
Donc écrire ma réponse à ce que disait pgeod de façon lisible c'est :
C=bar{(A,- p) ; ( B,-q) ; ( G,p+2q)}
ce n'est pas une réponse à ce que disait pgeod du tout
il parlait de la valeur du coefficient c dans G bary A(p) B(q) C(c)
toi tu parles du point C comme barycentre de tout à fait autres choses 
et tes calculs ne permettent même pas de répondre à la question de l'énoncé par une autre méthode que celle de pgeod...
oui.
et donc c'est le même coefficient qui a servi à définir I comme : I bary B(q) C(c) par pgeod
donc en fait ce point I là c'est bary B(q) C(q)
et donc où est il ce point I ?
la démonstration, en mots, était à comprendre ainsi :
I étant par définition (énoncé) sur la droite (AG) il existe un certain réel i tel que G =bar (A,p )( I, i)
I étant par définition (énoncé) sur la droite (BC) il existe un réel c tel que I = Bar (B,q) (C,c)
[ les calculs effectués ]
et maintenant on sait les valeurs de c (et donc la position de I sur la droite (BC), qui est la question à laquelle on demande de répondre dans l'énoncé )
et de i (mais on s'en fiche, i = 2q)