Bonjour!
Pouvez-vous m'aider, s'il vous plait! Me donner quelque piste. Je n'ai vraiment pas compris.
Merci d'avance!



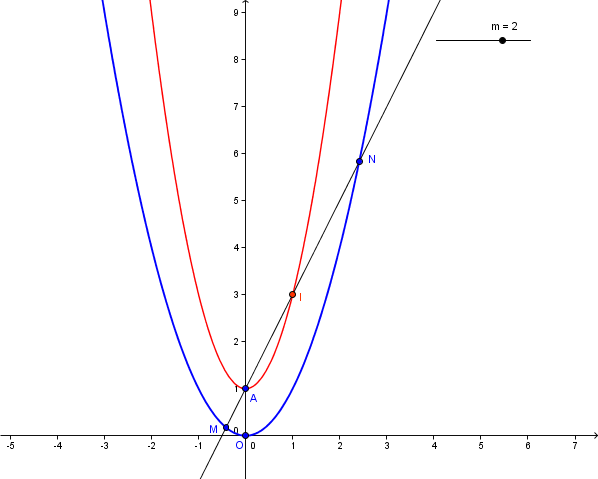
Dans un repère (0,i,j) on note P la parabole d'équation y=x² et A le point de coordonnées (0;1). Une droite d de coefficient directeur m passe par A et P en M et N.
Soit I le milieu du segment [MN] on veut examiner les positions successives du point I lorsque la droite d pivote autour de A.

1. Faire une figure; P et d se coupent-elles toujours en deux points? Quelle courbe semble parcourir le point I lorsque d varie? (Je n'arrive pas à commencer l'exercice)


2. Lorsque d pivote autour de A, on conjecture que M et N existent toujours. Prouvons-le.
Pour trouver les points d'intersection des deux courbes C₁> Et et C₂ d'équations y=f(x) et y=g(x), on raisonne en général de la façon suivante: dire que M, de coordonnées (α;β), appartient a l'intersection de C_f et C_g équivaut à dire que β=f(α) et β=g(α).
Donc α est solution de l'équation f(x)=g(x), dite "équation aux abscisses"
Démontrez que l'équation aux abscisses est x²-mx-1=0
Pourquoi cette équation a-t-elle toujours deux racines distinctes x₁ et x₂ ?


3. Si on note, par exemple, x₁ l'abscisse de M et x₂ celle de N, on sait trouver, en fonction de x₁ et x₂, les coordonnées (X₁;Y₁) du point I milieu de [MN]. Il est alors inutile de calculer x₁ et x₂
a) Vérifiez que X₁=x₁+x₂/2 et Y₁=m/2(x₁+x₂)+1

b) Déduisez-en, en fonction de m, les coordonnées du point I.


4. Pour trouver le lieu (L) de I, on essaie d'abord de trouver une relation entre X₁ et Y₁
a) Prouvez que I appartient à la parabole (C) d'équation y=2x²+1.

b) Réciproquement, il reste désormais à répondre à la question suivant: "Le point I décrit-il toute la courbe (C)"
Lorsque m décrit , prouvez que X₁ décrit et déduisez-en que I décrit toute la courbe (C).