Inscription / Connexion Nouveau Sujet
barycentre triangle et aire pour lundi 08/01 merci davance
coucou!! je narrive pa se devoir maison! c tres important pour moa merci de maider :d!! je ne comprend pa! il sagit de démontrer que M est le barycentre et il faut bien rédiger :s! merci davance!
M est un point intérieur à un triangle ABC.
Démontrer que le point M est le barycentre des points pondérés (A ,a) (B,b) et (C, c) avec :
a =aire du triangle MBC
b = aire du triangle MAC
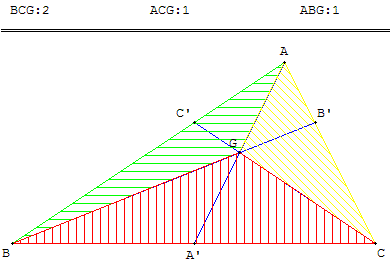
c = aire du triangle MAB ici figure
indication : on appellera A', B' et C' les points d'intersections respectifs de (AM) et (BC), de (BM) et (AC) et enfin de (CM) et (AB).
On pourra montrer que A' est le barycentre de (B ,aire de AA'C) et ( C, aire de AA'B)
bonjour! jai mis 1 image du triangle ds attacher! je narrive pa a démontrer que le point G est le barycentre! en plus il faut bien rédiger! merci davance de maider!!
G est un point intérieur à un triangle ABC.
Démontrer que le point G est le barycentre des points pondérés (A ,a) (B,b) et (C, c) avec :
a =aire du triangle GBC
b = aire du triangle GAC
c = aire du triangle GAB
indication : on appellera A', B' et C' les points d'intersections respectifs de (AG) et (BC), de (BG) et (AC) et enfin de (CG) et (AB).
On pourra montrer que A' est le barycentre de (B ,aire de AA'C) et ( C, aire de AA'B)
*** message déplacé ***
orely22,
comme tu as pu le lire lors de ton inscription, le multi-post n'est pas toléré sur ce site. Merci d'en prendre note.
Si tu penses que ton exercice est parti dans les profondeurs du forum, poste un petit message dans ton topic, il remontera parmi les premiers.
bonjour Orely,
Soit h la hauteur du triangle ABC issue de A,
Posons comme convention d'écriture : Aire (ABC) = ABC
On a : A' bary de B(A'C) et C(BA')
<=> A' bary de B(A'C*h) et C(BA'*h)
<=> A' bary de B(A'C*h/2) et C(BA'*h/2)
<=> A' bary de B(AA'C) et C(AA'B) (3)
De la même manière, dans le triangle AA'C, on a :
M bary de A'(AMC) et A (A'MC) (1)
De la même manière, dans le triangle AA'B, on a :
M bary de A'(AMB) et A (A'MB) (2)
En ajoutant membre à membre les égalités (1) et (2), on obtient :
M bary A'(AMC+AMB) et A(A'MC+A'MB)
<=> M bary A'(ABC), A'(-BMC), A(MBC)
or d'après (3), A' bary de B(AA'C) et C(AA'B)
donc M bary B(AA'C), C(AA'B), A'(-BMC), A(BMC)
<=> M bary B(AMC), B(A'MC), C(AMB), C(A'MB), A'(-BMC), A(MBC)
<=> M bary B(b), C(c), A(a), C(A'MB), B(A'MC), A'(-BMC)
or dans le triangle BMC, on a A' bary de B(A'MC) et C(A'MB)
donc M bary B(b), C(c), A(a), A'(BMC), A'(-BMC)
<=> M bary B(b), C(c), A(a)
...


