Bonjour
si tu prends les mêmes données angulaires pour la construction de ce parallélogramme mais avec des longueurs LE différentes, tu pourrais construire tous ces parallélogrammes et tu verrais que les angles LUE seraient à chaque fois différents.
Les formules qui lient les éléments du triangle LUE ne sont vraiment pas de ton programme.
Par conséquent, à mon humble avis,  c'est avec le rapporteur seulement que tu peux déterminer l'angle LUE

Bonjour Etoile.
Où est le point U ?
S'il s'agit de l'angle LIE, il est égal à 180° - angle ELI - angle LEI.

bonjour à tous les 2,

Pour répondre à PLUEMETEORE le point U et le centre de mon parallélogramme;
Ce point une fois tracé dans le parallélogramme devient le milieu LI (sachant que LEI forme un triangle).

LEI = 25°ILE = 55°
J'en ai déduit que LIE était = à 100°
Mais comment trouver la mesure de l'angle LUE et ensuite EUI (sans rapporteur)

Merci

JE VOUS JOINS LA CONSTRUCTION QUE J'AI PU REALISER AVEC LES INFORMATIONS DONNEES; CELA VOUS PERMETTRA DE VISUALISER MA PROBLEMATIQUE;

merci

moi ma reponde l'escice est vrai

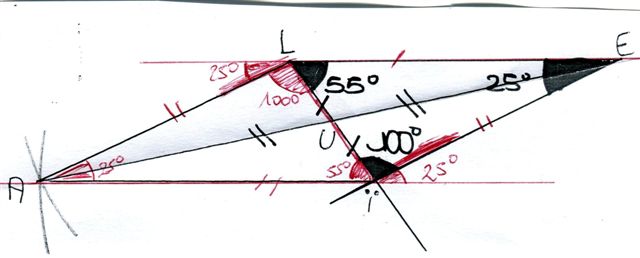
Bonsoir Etoile.
Ce problème me semble d'un niveau supérieur à la cinquième.
Néanmoins, voici une solution.
La perpendiculaire de E à (LI) rencontre (LI) en H, qui est extérieur à [EI], puisque l'angle EIL est obtus.
Les angles LEH, EIH et IEH valent respectivement 35°, 80° et 10°.
HL/HE = tan35); HI/HE = tan10°
HL/HI = tan35°/tan10°
HL = HI*tan35°/tan10°
IL = HL-HI = HI*[(tan35°/tan10°)-1]
HU = HI+IU = HI+(IL/2) = HI + HI*[(tan35°/tan10°)-1]/2 = HI*(1 + tan35°/tan10°)/2
tan HEU = HU/HE = HI/HE * (1 - tan35°/tan10°)/2 = tan10°*(1 + tan35°/tan10°)/2
angle HEU = 23,666°; angle EUI = 90° - angle HEU = 66,334°