Inscription / Connexion Nouveau Sujet
Calcul d'angle orienté
Bonjour à tous et bonne vacance aux concernés,
j'ai un devoir maison où je n'arrive pas à avancer donc je viens faire appel à votre aide, voici l'énoncé :
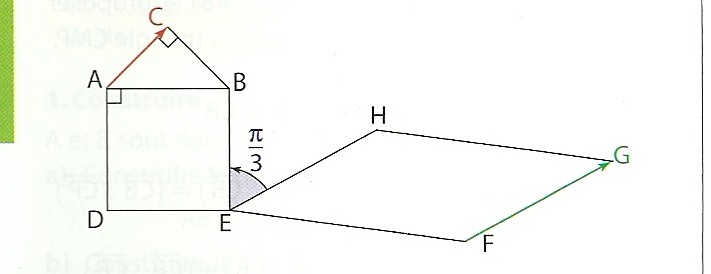
Sur la figure suivante, ABC est un triangle rectangle isocèle en C et direct, c'est-à-dire que (AD;AB) =  /2
/2
ADEB est un carré et EFGH un parallélogramme tels que :
(AD;AB) =  /2 et (EH;EB) =
/2 et (EH;EB) =  /3
/3
Le but de l'exercice est de calculer les mesures de l'angle orienté (AC;FG)
a) Justifier l'égalité :
(AC;FG)=(AC;AB)+(AB;AD)+(AD;FG)
b) Les mesures des angles (AC;AB) et (AB;AD) sont connues. Quelles sont-elles ?
=> Pour celle-ci je n'ai pas de problème
c) Justifier l'égalité (AD;FG)=(BE;EH)
En déduire une mesure de cet angle.
d) Terminer le calcul demandé
J'ai vraiment du mal avec la justification d'égalité car je ne sais jamais par où commencer...
Votre aide sera la donc la bienvenue ! Merci d'avance à ceux qui prendront le temps de m'aider.
Ps: Je risque de répondre avec un peu d'intervalle à chaque fois car je ne peux pas rester devant l'ordinateur toute la journée
(AC;FG)=(AC;AB)+(AB;AD)+(AD;FG)
c'est l'application directe de la relation de Chasles dans les angles orientés
Bonjour dhalte, je ne comprends pas cette égalité et je sais encore moins comment la démontrer. Pourrais-tu m'aider stp ?
c'est inquiétant, c'est le fondement même du cours sur les angles orientés...

Dans une version simple, tu rajoutes des partout pour traduire le fait qu'on peut aussi faire plusieurs tours complets sans changer fondamentalement cette relation.
Je suis tout à fait d'accord avec toi mon niveau en mathématiques est inquiétant mais que veux-tu que j'y fasse... Je fais des efforts mais sa marche pas. Sinon merci à toi pour ces explications
quoi, tu n'y arrives pas ?
tu n'arrives pas à justifier l'égalité suivante ?
tu n'arrives pas à utiliser la relation que je t'ai rappelée ?
donc
il suffit de remarquer que joue le rôle de
ça ressemble à la relation de Chasles dans les vecteurs, tu n'as jamais tâté de celle-ci non plus ?
et
donc
Pourrais-tu juste m'aider afin que je finisse cette exercice pour faire le petit c). C'est la même méthode que le a) ?
Ok :
Pour l'angle (AC;AB) :
ABC est un triangle rectangle isocèle en C et direct, d'où (CA;CB) =  /2
/2
Donc on applique la règle qui dit que dans un triangle la somme des angles vaut 
 - (
- ( /2) =
/2) =  /2
/2
( /2)/2 =
/2)/2 =  /4
/4
L'angle (AC;AB) vaut donc  /4
/4
Pour l'angle (AB;AD) =
ADEB est un carré donc les 4 angles qui le composent valent  /2
/2
(AB;AD) vaut donc  /2
/2
j'ai bien fait de vérifier
tes réponses sont justes, en classe de Quatrième, où on n'envisage que des angles non orientés.
Ici, on parle d'angles orientés.
La figure montre un angle qui affiche une flèche du coté de
cette flèche impose le sens de lecture des angles, qu'on appelle conventionnellement sens trigonométrique.
Dans tous les exercices, sauf éventuellement les plus tordus, ce sens sera toujours le même : le sens inverse de celui des aiguilles d'une horloge.
et si tu envisages l'angle orienté opposé :
et bien cet angle a une mesure opposée à celle de
de la même manière, a bien une mesure de
car cet angle est lu dans le sens trigonométrique.
mais on te demande une mesure de l'angle opposé :
de la même manière, on a
est-ce que tu as seulement lu ton cours avant de te lancer dans la résolution de ces exercices ?
Bonjour, je suis en première S et j'ai cet exercice en dm, on me demande de savoir par ces figures, en utilisant une décomposition par une relation de Chasles écrite en angles orientés, déterminer les mesures d'angle orienté (AC--> ; FG-->)
J'ai besoin d'aide svp


