Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première Angles orientésTopics traitant de angles orientés [tout]Lister tous les topics de mathématiques
Niveau première
Partager :

Calcul de cos pi/8 et sin pi/8

Posté par
Math_1 21-11-11 à 20:15

Bonjour, pourriez vous m'aider sur cet exercice?

C est le cercle trigonométrique associé à un repère orthonormé direct (O,I,J) du plan.
M est le point de C tel que (OI,OM)= pi/4 (2pi)
(On a OH hauteur du triangle OMI)

1.Quelles sont les coordonnées de M dans le repère ?
2.Calculer la distance IM
3.Démontrer que IM= 2 X sin pi/8

1. M(racine de 2/2 ; racine de 2/2)
2. je bloque car je ne vois pas comment utiliser le point H.
3. je ne vois pas comment démontrer.

Merci de votre aide

Posté par
dhaltere : Calcul de cos pi/8 et sin pi/8 21-11-11 à 20:18

quelles sont les coordonnées de H ?

ensuite : triangle rectangle : Pythagore

Posté par
Math_1re : Calcul de cos pi/8 et sin pi/8 21-11-11 à 20:19

Les coordonnés de H ne sont pas données...

Posté par
dhaltere : Calcul de cos pi/8 et sin pi/8 21-11-11 à 20:29

effectivement, mais tu es un petit gars intelligent, et je suis sûr que tu vas les trouver.

Posté par
Math_1re : Calcul de cos pi/8 et sin pi/8 21-11-11 à 20:38

Je suis une fille et les coordonnées de H sont cos de pi/8 et sin pi/8 ?

Posté par
dhaltere : Calcul de cos pi/8 et sin pi/8 21-11-11 à 20:48

comment la jeune fille qui y tient a-t-elle trouvé les coordonnées de M ?

toute seule, comme une grande ?

alors elle expliquera au monde ébahi pourquoi elle n'arrive pas à trouver les coordonnées de H ?

c'est tellement gros (je parle maths, là, pas de tour de tête)

M(\frac{\sqrt2}2;\frac{\sqrt2}2) \\ \\ H(\frac{\sqrt2}2;0)

Posté par
Math_1re : Calcul de cos pi/8 et sin pi/8 21-11-11 à 20:54

Je m'excuse je me suis mal exprimé sûrement:
Le point H se trouve sur le segment MI et non OI.
Ce qui je pense explique le fait que je n'arrive pas à exprimer ses coordonnées.
Merci de la réponse quand même.

Posté par
dhaltere : Calcul de cos pi/8 et sin pi/8 21-11-11 à 21:03

oui, un graphique aurait évité la méprise

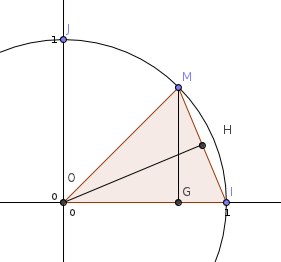
Calcul de cos pi/8 et sin pi/8

I(1;0) \\ M(\frac{\sqrt2}2;\frac{\sqrt2}2)

Pythagore là aussi en considérant le triangle MGI, rectangle en G

IM=\sqrt{(\frac{\sqrt2}2-1)²+(\frac{\sqrt2}2-0)²}=\sqrt{2-\sqrt2}

Posté par
Math_1re : Calcul de cos pi/8 et sin pi/8 21-11-11 à 21:05

Merci de votre aide.

Posté par
Moi96re : Calcul de cos pi/8 et sin pi/8 19-03-12 à 18:07

IM=\sqrt{(\frac{\sqrt2}2-1)%B2+(\frac{\sqrt2}2-0)%B2}=\sqrt{2-\sqrt2}

Posté par
dhaltere : Calcul de cos pi/8 et sin pi/8 20-03-12 à 07:50

ça va ? tu as fait ta petite expérience ?

tu peux utiliser le bouton "Aperçu" sans avoir besoin de poster

et si tu veux un résultat satisfaisant, entoure le texte des balises tex, comme ceci :

[tex]IM=\sqrt{(\frac{\sqrt2}2-1)²+(\frac{\sqrt2}2-0)²}=\sqrt{2-\sqrt2}[/tex]

tu obtiendras ceci
IM=\sqrt{(\frac{\sqrt2}2-1)²+(\frac{\sqrt2}2-0)²}=\sqrt{2-\sqrt2}

Posté par
Moi96re : Calcul de cos pi/8 et sin pi/8 20-03-12 à 12:58

Euh vraiment désolé. Merci pour l'info.

Posté par
dhaltere : Calcul de cos pi/8 et sin pi/8 20-03-12 à 13:02

heureux d'avoir pu t'être utile.

Posté par
tomhippore : Calcul de cos pi/8 et sin pi/8 24-03-12 à 11:20

Bonjour,
j'ai aussi cet exercice à faire.
Après avoir trouver IM, il faut démontrer que IM= 2*sin(pi/8). Là je sèche...

Posté par
Moi96re : Calcul de cos pi/8 et sin pi/8 24-03-12 à 11:32

(OM,OI) = (OM;OH) + (OH,OI) = 2 × (OM,OH)
Donc (OM,OH) = (OM,OI)/2 =/8
OHM est un triangle rectangle en H
On peut donc voir que MH est le côté opposé à /8
OM est l'hypoténuse de ce triangle OHM
Donc sin  /8 = MH/OM
Donc MH =sin/8
Et comme IM= 2×MH
IM=2×sin/8

C'est ce que j'ai marqué dans mon DM.

Posté par
Moi96re : Calcul de cos pi/8 et sin pi/8 24-03-12 à 11:32

Et oublie pas les flèches sur les vecteurs

Posté par
tomhippore : Calcul de cos pi/8 et sin pi/8 24-03-12 à 11:42

Merci ! Je ne pensais plus du tout au calcul d'angle de type (OM,OI) = (OM;OH) + (OH,OI) = 2 × (OM,OH), vu qu'on a fait ce chapitre vers novembre !
Merci bonne journée

Posté par
Moi96re : Calcul de cos pi/8 et sin pi/8 24-03-12 à 13:33

Il n'y a pas de quoi Bonne journée à toi aussi.

Posté par
tomhippore : Calcul de cos pi/8 et sin pi/8 24-03-12 à 13:41

Et pour trouver IM tu avais utilisé la méthode du dessus (avec un triangle MGI) ou tu avais utilisé H? Au quel cas je ne sais pas comment faire pythagore avec ce point H, il manque une mesure j'ai l'impression...

Posté par
dhaltere : Calcul de cos pi/8 et sin pi/8 24-03-12 à 19:52

J'avais écrit

I(1;0) \\ M(\frac{\sqrt2}2;\frac{\sqrt2}2)

Pythagore là aussi en considérant le triangle MGI, rectangle en G

IM=\sqrt{(\frac{\sqrt2}2-1)²+(\frac{\sqrt2}2-0)²}=\sqrt{2-\sqrt2}

il y a quelque chose que tu ne comprends pas ?

Posté par
tomhippore : Calcul de cos pi/8 et sin pi/8 24-03-12 à 21:53

Si j'ai compris merci!

Posté par
tomhippore : Calcul de cos pi/8 et sin pi/8 25-03-12 à 12:07

Encore une petite question ! Comment définir le point H? OH est quoi? La bissectrice de l'angle IOM ou la hauteur à MI issue de O?

Posté par
dhaltere : Calcul de cos pi/8 et sin pi/8 25-03-12 à 13:23

les quatre mon colon, puisque OIM est isocèle de sommet O :
- OH médiane passant par O
- OH médiatrice de [IM]
- OH hauteur issue de O
- OH bissectrice de l'angle \widehat{IOM}
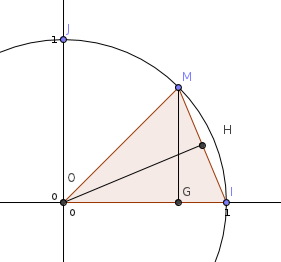
Calcul de cos pi/8 et sin pi/8

Posté par
tomhippore : Calcul de cos pi/8 et sin pi/8 25-03-12 à 16:37

Merci, j'avais zappé que OM était aussi un rayon.
Pour calculer cos pi/8, je suis parti de cos x= sin (pi/2 + x)
Donc cos pi/8 = sin 5pi/8 mais comment calculer cela ?

Enfin, la dernière question, il faut donner des lignes trigonométriques ... Qu'est ce? Jamais entendu parler...

Posté par
dhaltere : Calcul de cos pi/8 et sin pi/8 25-03-12 à 17:05

les lignes trigonométriques se limitent aujourd'hui aux sinus, cosinus et tangente.
voir là : pour toutes les autres (schéma à droite dans la page wikipedia), mais aujourd'hui, elles sont oubliées des manuels scolaires, vous avez eu de la chance

pour le calcul des lignes de \frac{\pi}8, tu aurais pu envisager que le travail préparatoire te soit utile, non ? et tu as à ta disposition une bissectrice, non ?

Posté par
tomhippore : Calcul de cos pi/8 et sin pi/8 25-03-12 à 17:26

Oui j'ai effectivement une bissectrice...
Il y a un lien entre la bissectrice et cos pi/8?
Là je ne vois aucune relation...

Posté par
tomhippore : Calcul de cos pi/8 et sin pi/8 25-03-12 à 17:45

J'ai trouvé cos pi/8 = racine2/4 + 1/2 grâce à cos^2 + sin^2=1. C'est juste?

Posté par
tomhippore : Calcul de cos pi/8 et sin pi/8 25-03-12 à 17:52

Correction : cos pi/8 = (racine(racine 2)+2)/2. Juste?

Posté par
dhaltere : Calcul de cos pi/8 et sin pi/8 25-03-12 à 18:08

non

et je m'étonne : tu avais déjà la valeur du sinus pour envisager d'utiliser cette relation et trouver le cosinus ?

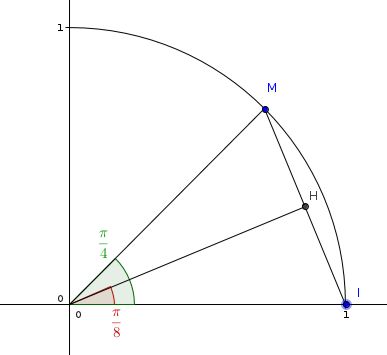
Calcul de cos pi/8 et sin pi/8

I a pour coordonnées (1;0)

\cos(\frac\pi8)=\dfrac{OH}{OI}

\sin(\frac\pi8)=\dfrac{IH}{OI}

M a pour coordonnées (\cos(\frac\pi4);\sin(\frac\pi4)) = (\frac{\sqrt2}2;\frac{\sqrt2}2)

H, milieu de IM, a pour coordonnées (\frac{\sqrt2}4;\frac{2+\sqrt2}4)

Par Pythagore, la longueur OH a pour valeur \frac12\sqrt{2+\sqrt2}

Par Pythagore, la longueur IH a pour valeur \frac12\sqrt{2-\sqrt2}

je n'ai pas reproduit les calculs intermédiaires, et te fais confiance pour terminer seul.

Posté par
dhaltere : Calcul de cos pi/8 et sin pi/8 25-03-12 à 18:14

ta correction donne la bonne valeur, mais tu m'expliqueras comment tu l'as obtenue

Posté par
tomhippore : Calcul de cos pi/8 et sin pi/8 25-03-12 à 18:30

Dans une question précédente, j'avais calculé sin pi/8= (racine(2-racine2)/2. La relation cos^2+sin^2=1 à fait le reste...
Pour la suite, on me demande d'en déduire les lignes trigo de 7pi/8, 9pi/8,5pi/8 et 3pi/8. Je crois qu'on peut tout résoudre avec des relations du genre sin(pi+x)=-sin x. Juste?

Posté par
dhaltere : Calcul de cos pi/8 et sin pi/8 25-03-12 à 18:52

et comment as-tu obtenu sin(pi/8) ?

oui, pour les autres, on peut

Posté par
LaBananere : Calcul de cos pi/8 et sin pi/8 01-04-12 à 10:04

Bonjour à tous !
Sujet oublié ? :'(
Finalement rien pour ce fameux sin(pi/8) ?
Sinon ça peut en aider certains, c'est le 84 p 250 de déclic mathématiques 1èreS

Posté par
dhaltere : Calcul de cos pi/8 et sin pi/8 01-04-12 à 10:08

Sujet oublié ?
pourquoi, tu as des soucis ?

Posté par
LaBananere : Calcul de cos pi/8 et sin pi/8 01-04-12 à 10:13

Serait-ce sin(pi/8)=(racinede(2-racinede2))/2 ?
Et si possible un peu d'explications pour la dernière question (en déduire les lignes trigo de 7pi/8, 9pi/8,5pi/8 et 3pi/8) me seraient d'un grand secours merci !

Posté par
dhaltere : Calcul de cos pi/8 et sin pi/8 01-04-12 à 10:22

dans le triangle OIH, rectangle en H, l'hypoténuse OI a pour longueur 1 et l'angle au sommet O est \frac{\pi}8
donc on a immédiatement \sin(\frac{\pi}8)=IH
et j'ai montré que IH=\frac{\sqrt{2-\sqrt2}}2
alors pourquoi hésites-tu ?

pour le reste, il suffit d'utiliser les relations que tu n'as évidemment pas vues en cours (vas-tu prétendre) qui sont

\cos(\pi-x)=-\cos(x)

\cos(\pi+x)=-\cos(x)

\sin(\pi-x)=\sin(x)

\sin(\pi+x)=-\sin(x)

\cos(\frac{\pi}2-x)=\sin(x)

\sin(\frac{\pi}2-x)=\cos(x)

\cos(\frac{\pi}2+x)=-\sin(x)

\sin(\frac{\pi}2+x)=\cos(x)

Posté par
LaBananere : Calcul de cos pi/8 et sin pi/8 01-04-12 à 10:24

Oui je les ai effectivement vu en cours *je suis un boulet*
Merci et désolé ^^

Posté par
LaBananere : Calcul de cos pi/8 et sin pi/8 01-04-12 à 10:28

Dernière question :
Est-ce donc normal qu'on ait cos(pi/8)=sin(pi/8) ? (en faisant avec la relation sincarré+coscarré=1)

Posté par
dhaltere : Calcul de cos pi/8 et sin pi/8 01-04-12 à 10:30

non, ce n'est pas normal

serais-tu en train de révolutionner les mathématiques ?
je pencherais plutôt pour une erreur de calcul.

Posté par
LaBananere : Calcul de cos pi/8 et sin pi/8 01-04-12 à 10:33

Ou alors cos(pi/8)=1/2(racinede(2-racinede2))/2) et sin(pi/8)=(racinede(2-racinede2))/2 plutôt non ?

Posté par
dhaltere : Calcul de cos pi/8 et sin pi/8 01-04-12 à 16:13

essaie encore une fois
(indice : la réponse est déjà dans mes messages précédents)

Posté par
fedjerre : Calcul de cos pi/8 et sin pi/8 18-04-12 à 08:48

bonjour
dhalte :
je ne comprends par comment tu obtiens xH=\normalsize \frac{\sqrt{2}}{4}

moi j'ai :
\normalsize \frac{\frac{\sqrt{2}}{2}+1}{2}=\frac{\sqrt{2}+2}{4}

(ce que tu obtiens en ordonnée!

Posté par
dhaltere : Calcul de cos pi/8 et sin pi/8 18-04-12 à 10:50

tu as raison, j'ai simplement interverti les coordonnées de H lors de ma recopie
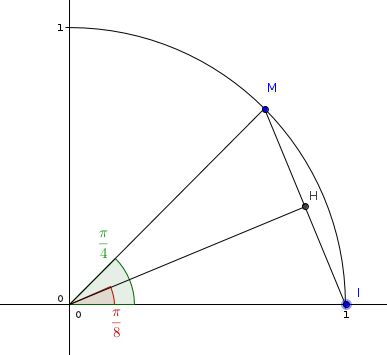
Calcul de cos pi/8 et sin pi/8
I a pour coordonnées (1;0)

\cos(\frac\pi8)=\dfrac{OH}{OI}

\sin(\frac\pi8)=\dfrac{IH}{OI}

or OI=1, donc

\cos(\frac\pi8)=OH

\sin(\frac\pi8)=IH

M a pour coordonnées (\cos(\frac\pi4);\sin(\frac\pi4)) = (\frac{\sqrt2}2;\frac{\sqrt2}2)

puisque les coordonnées de I sont (1;0)
H, milieu de IM, a pour coordonnées (\dfrac{\frac{\sqrt2}2+1}2;\dfrac{\frac{\sqrt2}2+0}2) =  (\frac{\sqrt2+2}4;\frac{\sqrt2}4)

donc
puisque les coordonnées de O sont (0;0)
OH = \sqrt{(x_h-0)^2+(y_h-0)^2}=\sqrt{(\frac{\sqrt2+2}4)^2+(\frac{\sqrt2}4)^2}=\frac12\sqrt{2+\sqrt2}

puisque les coordonnées de I sont (1;0)
IH = \sqrt{(x_h-1)^2+(y_h-0)^2}=\sqrt{(\frac{\sqrt2+2}4-1)^2+(\frac{\sqrt2}4)^2}=\frac12\sqrt{2-\sqrt2}

Et finalement
\cos(\frac{\pi}8)= \frac12\sqrt{2+\sqrt2}

\sin(\frac{\pi}8)= \frac12\sqrt{2-\sqrt2}

Posté par
fedjerre : Calcul de cos pi/8 et sin pi/8 18-04-12 à 13:20

OK merci
je suis aussi arrivé à ce résultat avec la relation cos²x + sin²x = 1

c'est plus simple non?

Posté par
dhaltere : Calcul de cos pi/8 et sin pi/8 18-04-12 à 13:37

plus simple ?

tu ne me donnes pas de détails, je ne sais pas si tes étapes de calcul ont fait que c'était plus "simple"

je suppose quand même que tu as dû faire à peu près les mêmes calculs, non ?

alors est-ce plus simple ?

un critère est celui-ci : si ça TE semble plus simple, retiens ta technique, elle TE sera plus facile à retenir qu'une autre qui ne te paraît pas plus simple.

mais si tu veux donner les détails, je pourrai toujours te les commenter, car ce qui te paraît plus simple l'est peut-être du fait de "simplifications" pas ou mal justifiées.

Posté par
fedjerre : Calcul de cos pi/8 et sin pi/8 18-04-12 à 18:26

cos²(/8)+sin²(/8)=1
\normalsize \frac{2+\sqrt{2}}{4}+sin²(pi/8)=1 \\ \\ sin²(pi/8)=1-\frac{2+\sqrt{2}}{4}=\frac{4-2-\sqrt{2}}{4}=\frac{2-\sqrt{2}}{4}


sin(/8)=\normalsize \frac{\sqrt{2-\sqrt{2}}}{2}

pour calculer cos (/8) mon exercice n'utilisait pas les coordonnées des points mais on utilisait I' (-1;0) et on se plaçait dans le triangle I'MH avec H le projeté orthogonal de M sur [OI]
tu dois connaître sans doute cette méthode aussi!

Posté par
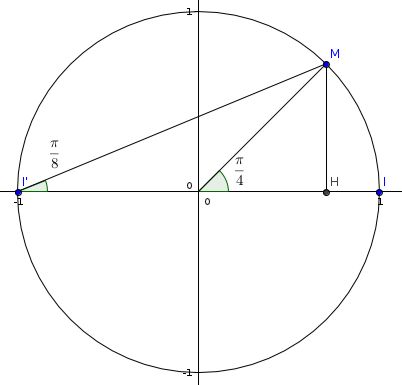
dhaltere : Calcul de cos pi/8 et sin pi/8 18-04-12 à 19:11

oui
Calcul de cos pi/8 et sin pi/8
l'angle au centre (ici \widehat{IOM}=\frac{\pi}4) est le double de l'angle inscrit, (ici \widehat{II'M}=\frac{\pi}8)

donc il te faut d'abord calculer l'hypoténuse
I'M=\sqrt{I'H²+HM²}=\sqrt{(1+\cos(\frac{\pi}4))²+\sin(\frac{\pi}4)²}=\sqrt{2+\sqrt2}

puis tu peux calculer
\cos(\frac{\pi}8)=\frac{I'H}{I'M}

et enfin le sinus
\sin(\frac{\pi}8)=\frac{HM}{I'M}
mais tu as choisi de passer par \cos²+\sin²=1

tu veux mon avis ?
je préfère largement la première méthode...

Posté par
fedjerré 18-04-12 à 22:24


Rechercher
Menu
Espace membre
32 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1719 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !