Inscription / Connexion Nouveau Sujet
Calcul de limite
Bonjour à tous, je suis nouveau sur le site et ceci est mon premier topic. Je suis en terminal S et n'ayant pas bosser l'année derniére, j'éprouve donc des difficultés cette année à "rattraper le niveaux".
Alors voici mon probléme : Ma prof de math a décidé de nous faire un rappel sur les limites et nous a donc donné quelques calculs de limites et je me rend compte que j'ai vraiment des difficultés et que j'aurais du bosser l'année derniére 
, Voici l'exercice ou je bloque :
Calculer la limite de f(x)=(-2x)\(x²+x-2), x appartient à ]1;+(infinie)[ (désolé je ne sais pas comment insérer des termes mathématiques 
)
Je calcul donc la limite de (-2x)/x² quand x tend vers + l'infinie, que je simplifie en -2/x et je trouve donc lim-2/x=0 Et je bloque a cette endroit ... Est-ce possible que la limite soit 0 ? Si oui comment fait-on le reste du calcul ?
Voila, merci pour vos réponse
Bonsoir flow09
Tu t'es servie de la propriété : Un quotient de 2 fonctions polynômes a aux infinis la même limite que le rapport des termes de plus haut degré (avec leur coefficient)
Donc c'est juste de dire que f(x)=(-2x)/(x²+x-2) a en +
la même limite que -2x/x² , ou encore après simplification , que -2/x
La limite de -2/x en + est bien 0 , donc
lim f(x) = 0
x
+
A retenir
Si num l et dén , alors la limite du quotient est 0
Merci Elisabeth67 pour ta réponse, maintenant je doit calculer la limite de f quand x1 et trouver si il y a une asymptote or je n'ai aucune idée de la méthode a suivre. Si quelqu'un pourrait m'éclaicir a ce sujet se serais gentil, merci d'avance
En 1+ ( d'après le domaine de définition , on doit étudier la limite uniquement en 1 , avec x > 1 ), le numérateur tend vers -2 , et le dénominateur tend vers 0 .
Il faut déterminer s'il s'agit de 0- ou 0+
Le polynôme x²+x-2 s'annule en -2 et en 1 , entre ces 2 valeurs , il est négatif , et positif si x < -2 ou x > 1 ( fais-toi un petit tableau de signes )
Alors revenons au quotient ; le num -2 et le dén 0+ , donc ce quotient va tendre vers -
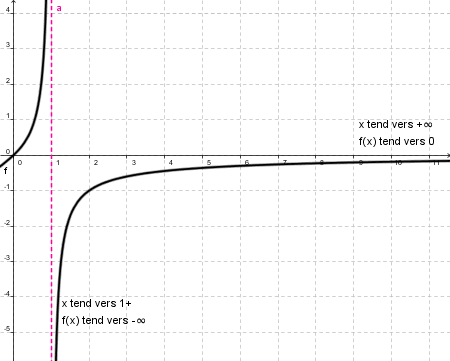
Sur la représentation graphique , tu peux retrouver ces résultats
Merci beaucoup sa commence a revenir ^^ maintenant je n'ai plus qu'à faire les 15 autres calculs merci encore et bonne soirée
J'ai un nouveau probléme sur un calcul : je dois calculer la limite de (x²+x-
x)/(x²+1) lorsque x appartient à 
La racine carré me géne et m'empéche de faire le calcul (je suis vraiment nul ...)
Rebonjour !
L'ensemble de définition de cette fonction est [0;+[ ( à cause de x )
En +
Toujours la même propriété :Un quotient de 2 fonctions polynômes a aux infinis la même limite que le rapport des termes de plus haut degré (avec leur coefficient)
Ici , le terme de plus haut degré du numérateur est x² et le terme de plus haut degré du dénominateur est x²
Conclusion ?
En 0 , pas de problème , la fonction est définie , donc
limf(x) = f(0) = 0
x0
Annuler
connectez vous