Inscription / Connexion Nouveau Sujet
Calcul de Volume complexe
Salu
Je bloque sur un de mes exos de mon DM!! J'aurais besoin d'un coup de main!! Je vous remercie d'avance pour toute l'aide que vous pourrez m'apportez!
Le but est le calcul du volume d'une ampoule
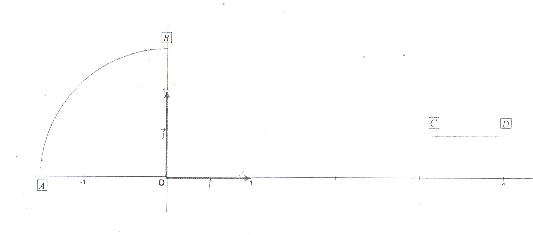
Dans le plan muni d'nu repère orthonormal (O;
;smb]vectj[/smb]) (unité: 2 cm), on donne les points:A,B,C et D (Voir le fichier joint) et l'ar de cercle AB de centre O comme l'indique la figure
1.On veut raccorder l'arc AB au segment [CD] par une courbe admettant en B la meme tangente que l'arc de cercle et tangent en C a la droite (CD)
Soit la fonction f définie sur [0;
] par: f(x)=(1/2)cosx+1
a) Démontrer que la courbe d'équation y=f(x) repond aux conditions posées
b) Tracer cette courbe, l'arc AB et le segment [CD] dans le repère (O;;smb]vectj[/smb])
2. Démontrer que pour tout réel x:
[(1/2)cosx+1]² = [(1/8)cos2x+cosx+(9/8)]
3. Soit 
l'ensemble des points du plan délimité par l'arc de courbe ABC, l'axe (Ox) et la droite d'équation x=
Calculer le volume V du solide re révolution engendré par la rotation de autour de l'axe (Ox). Donner la valeur exacte de V en cm3
Je vous joint les coordonnées des point A,B,C et D, ainsi que la figure!!
Et encore merci pour l'aide que vous m'apporteez!
Pour le 2 :
[(1/2)cosx+1]² = 1/4 (cosx)^2 + cosx + 1
Or (cosx)^2 = 1/2 + 1/2 cos2x (formule de duplication)
D'ou [(1/2)cosx+1]² = [(1/8)cos2x+cosx+(9/8)]
Pour le 1 il faut que tu vérifies que f coincide avec les points B et C c'est a dire que f(0)=3/2 et f(pi) = 1/2
D'autre part il faut que la courbe de f admette en B la meme tangente que l'arc de cercle c'est à dire une droite de coefficient directeur nul donc il faut que
f'(0)=0
De meme il faut que la courbe de f admette en C la droite (CD) pour tangente c'est à dire une droite de coefficient directeur nul donc il faut que
f'(pi)=0 ....
Je te laisse vérifier ... 
Merci beaucoup pour ton aide!! C'est mon mon exo est terminé^^
Est ce que quelqu'un pourrais répondre à la 3)ème question du sujet s'il vous plait d'avance merci.
Dans le sujet que j'ai, il rappelle que le volume d'une demi boule est:
(2/3)pi.r^3
up, merci de m'aider pour la question 3, précision :
On a rappellé que le volume d'une demi boule est :
2/3.pi.r^3
Faudra t'il encore multiplier cette expression par 8 (produit des trois vecteurs unitaires du repère) pour obtenir l'aire de la demi boule en cm^3, car avec l'expression rappelée, je pense que c'est exprimé qu'en unité de volume (u.v) comme les intégrales.
Merci de votre attention 
bonjour mateo8810
est-ce un exo de 1° ?
pour le calcul du volume j'utilise une intégrale de f(x) pour 0<x<pi :
Volume = volume 1/2 boule + 0.Somme.pi( pi.( f(x) )².dx )
mais, en 1°, tu n'es pas sensé avoir vu les intégrales...
Peux-tu confirmer le niveau de ton exo ainsi que le tien, s'il te plaît ?
.
Bonjour mikayaou,
je suis effectivement en terminale S et j'ai cet exercice en devoir maison. Or j'ai trouvé cet exercice dans le forum de 1ère, qui il est vrai date de 2 ans, les premières il y a deux ans devaient peut-être avoir ça dans leur programme, bref.
Je vais vérifier de mon côté mes résultats pour comparer aux tiens après mais le volume que tu m'a donné la, c'est en unité de volume pas vrai ? Il reste à passer en cm^3 en multipliant par 2*2*2 ?
effectivement mateo8810, si l'unité sur les axes est de 2cm, le volume sera de (sauf erreur) 9(2+pi)pi cm^3
A vérifier
.
C'est bon, j'ai vérifié en fesant le calcul d'intégrale etc.. on obtient bien :
9(2+)/8 en u.v
puis 9(2+) en cm^3
Merci de ton aide !!
Annuler
connectez vous