Inscription / Connexion Nouveau Sujet
Calcul (et explication de x0)
Re bonjour.
Pour la suite de mon DM, j'ai cet exercice aussi.
Un industriel fabrique et commercialise des jouets. On suppose tout au long de cet exercice qu'il n'a pas d'invendus dans sa production.
On désigne par x le nombre de centaines de jouets fabriqués.
Le coup total de la fabrication est donnée en centaines d'euros par Ct(x)=0,03x^3 -0,45x² +2,5x
Si l'industriel fabrique x centaines d'objets , il vend chaque centaine de jouet au pris P(x)= 2-0,08x
La production est comprise entre 100 et 1000 jouets.
1)Calculez la recette totale R(x) pour la vente de x centaines de jouets.
2)Rappelons que les économistes assimilent le cout marginal Cm à la dérivé du coup total Ct. De même , on a coutume d'assimiler la recette marginale Rm a la derivé de la recette total
Calculer pour quel valeur x0 de x la recette marginale est egale au cout marginal.
On donnera x0 à 10 jouets pres
Je ne sais pas ce que c'est x0, mais j'ai avance avec:
Rm=R'(x) = 2-0,16.x
Cm = C'(x) = 0,09x²-0,90x+2,5
Donc, a priori je devrai faire:
2-0,16x = 0,09x²-0,9x+2,5
Je trouve:
0,09x²-0,74x+0,5=0
Je bloque pour la suite
3)Verifier que le benefice est maximal en x0.
Le benefice = recette - cout
Donc:
(2x-0,08x²) -(0,03x^3 -0,45x² +2,5x) = benefice
Je suppose que je dois faire la derivee et calculer , x1 et x2?
, x1 et x2?
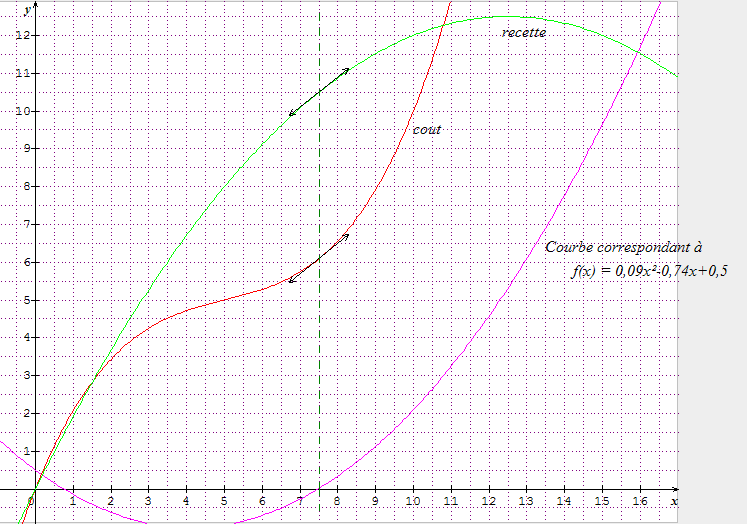
4) Representez les fonctions Ct et R sur une calculette graphique:
En observant le graphique, que peut on conjecturer pour les tangantes à ces deux courbes au point d'abscisse x0?
Expliquer pourquoi ce résultat est vrai?!
Je n'ai pas encore fais cela, je ne suis pas sur de comprendre.
Merci d'avance
bonsoir,
x0 est seulement le nom qu'on donne à une valeur particuliere de x, ici celle pour laquelle la recette marginale est egale au cout marginal.
mais tu gardes x dans les equations si cela te gêne 
2) tu as la bonne demarche .
tu arrives à une equation du second degré.
tu sais calculer un discriminant? ... oui? c'est le moment de l'utiliser !

3) là tu dois juste remplacer x dans l'expression du benefice par la valeur x0 trouvee à la question precedente
4) tu traces la tangente à ces deux courbes au point d'abscisse x0 solution de la question 2).
il se trouve que le coef directeur de la tangente en x0 est justement la derivee en x0 .
donc pour la premier courbe, le coef directeur de sa tangente est C'(x0) et pour la deuxième courbe c'est R'(x0) .
D'apres la definition de x0 ces deux valeurs sont egales.
Merci Sariette,
J'etais pas trop loin et tes explications complementaires ont confirme ce que j'avais fait et la reponse 4 m'avance bien. Je pense qu'avec cela ca ira.
Merci beaucoup
Svpp jaimré bien avoir la reponse a la premiere kestion ^^
1)Calculez la recette totale R(x) pour la vente de x centaines de jouets.
bonsoir,
P(x)= 2-0,08x est le prix de vente pour une centaine d'objets
si il y a x centaines cela fait une recette de R(x) = x * P(x) = 2x-0,08x²
merci pr la réponse mais c un pe tro tard g deja tt fai ....mais merci kan mm c tres gentil dta part 
parce que moi j'ai trouvé deux valeurs (non tout à fait égale) :
x1 = 0.74 et x2 = 1.34
la question demandait de donner qu'Une seule valeur donc je crois que je me suis trompé.
Aider moi svp
bonsoir,
désolée je ne vois ton message que maintenant ...
toujours le problème des vieux topics qui remontent.
moi je trouve une seule valeur de x positive qui est : soit x0 = 7,48 environ, ce qui correspond au dessin ( abscisse du point où les tangentes sont parallèles)