Inscription / Connexion Nouveau Sujet
calcul longueur dans une pyramide à base rectangulaire
Bonjour, j'ai un exercice de 5 questions noté a rendre pour mardi :
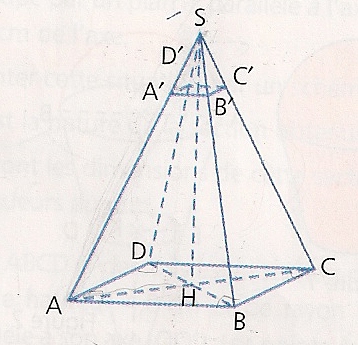
j'ai une pyramide SABCD à base rectangulaire ABCD dont les diagonales se coupent en H (H est donc le milieu du rectangle)
S est le sommet
SH est la hauteur qui mesure 12cm
Puis j'ai une réduction de cette pyramide à base rectangulaire SA'B'C'D'. Dans celle ci je ne connais aucune mesure.
AB = 8 cm / BC = 6cm / SH = 12cm
1) calculer la longueur AC puis AH :
j'ai calculé AC grace au théorème de Pythagore = 10 cm
j'ai déduis que AH = AC : 2 = 5cm
2) calculer le volume de la pyramide SABCD :
je l'ai fait : 192 cm3
3) Calculer la longueur SA :
c'est à cette question que je bloque :
si j'utilise le théorème de thalès dans le triangle SAB : il me manque les longueurs du petit triangle donc impossible
si je travaille dans le triangle SAH le triangle n'est pas rectangle alors je ne peux utiliser le théorème de Pythagore
Le problème est que la question 4 est impossible si on ne connait pas la longueur SA
5) on coupe la pyramide SABCD par un plan parrallèle à la base et passant par un point E du segment [SA] tel que le volume de la pyramide obtenue est 8 fois plus petit que celui de la pyramide SABCD. Il faut calculer la longueur SE
je pense qu'il faut diviser le volume de la grande pyramide (192cm3) par 8 soit 24cm3. Ce n'est qu'une supposition
Merci de votre aide préciseuse !
Mais c' est quoi ce dessin ?
Les mesures ont été divisées par 2
si on prend k le coeff de réduction = 1/2
on se retouve avec toutes les mesures divisées par 2
1/3 * 4 * 3 * 6 = 24 cm3
§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§
Pourquoi " 2 "
Pour un volume : (1/2)3 = 1/8
Le dessin est celui de mon manuel de maths.
et comment tu peux me dire que les mesures ont été divisées par 2 ? Je ne comprends pas pourquoi tu mets pour un volme (1/2)3 = 1/8 ?
Sinon aujourd'hui j'ai vu mon prof de maths qui m'a dit que le volume V' de la petite pyramide est égal à k3V
et donc il faut que je prouve que k3 = 1/8
Merci
Non elle n'est pas représentée car dans la question c'est 'on place un point E sur le segment SA à 3.25 cm de S et on met un plan parralèle à la base passant par E, calculer le volume de cette pyramide'
D'ailleurs je me suis trompée en haut c'est SA Qu'il faut calculer, j'ai réussie !
Mais pourquoi si on prend k le coef de reduc = 1/2
Il vient d'ou le 1/2 ? Pourquoi tu divises les longueurs par 2 ?
Oui je suis d'accord 1/23 = 1/8. Mais pourquoi si on prend k le coef de reduc = 1/2
c'est cela que je ne comprends pas
Divisé par 2
ou
multiplié par 1/2
c' est pareil .
On calcule la longueur SA = 13 cm
et on regarde la réduction puisqu' on connaît
la longueur SE = 3,25
k = 1/4
On est mal pour la réduction de 8 fois moins ?
Bonjour,
Si ta pyramide était un cube...
par exemple de coté 2
Son volume serait 2x2x2 =8
si tu divises son coté par 2
son volume sera 1 (1x1x1)=1
donc divisé par 8....
si k = 1/2 c'est normal que le volume soit 8 fois plus petit soit V' = 1/8 Vsabcd = 24cm3
et si on fait 192 (volume de sabcd) : 8 = 24
donc SE = SA x 1/2
= 6.5 cm
Je pense que c'est correct non ?
Il faut savoir si on part de 8
k3 = 1/8
donc : k le coeff de réduction = 1/2
Si le volume de la petite pyramide en réduction
est 8 fois plus plus petit , oui on divise par 2 :
SA = 6,5 cm
§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§§
Mais tu parlais ce matin de SA = 3,25 cm ?
Il y a eu un embrouillage. Voici la question recopiée :
5) On coupe la pyramide par un plan parrallèle à la base et passant par un point E du segment [SA] tel que le volume de la pyramide obtenue est huit fois plus petit que celui de la pyramide SABCD. Calculer la longueur SE
AB : 8cm
BC : 6 cm
SH : 12 cm
SA' : 3.25 cm
SA: 13 cm (longueur calculée)
AC : 10 cm (longueur calculée)
AH : AC : 2 = 5cm (longueur calculée)
-------------------------------------------------------------------------------------------------------------------------
Je pense que pour calculer SE :
- on multiplie SA par le facteur k : 1/2 soit 1/8 au cube
- 13 x 1/2 = 6.5 cm
Je ne comprends pas : SA' = 3,25 cm
On en reste à k3 = (1/2)3
On trouve 192 / 8 = 24 de cette manière :
toutes les mesures sont divisées par 2
V' = 1/3 * 8/2 * 6/2 * 12/2
V' = 1/3 * (8 * 6 * 12)/(2 * 2 * 2)
V' = 1/3 * 576/8
V' = 192/8
V' = V/8
ou : V' = (1/8)V
Oui d'accord toutes les mesures ont été : par 2
mais par contre SA' c'est pas moi qui l'ai inventé !! 
en faite : sur le segment SA il y a un point A' qui est situé a 3.25cm du sommet S et en dessous (normalement selon nos calculs) E qui est situé au milieu du segment SA
SE = SA : 2 = 6.5 cm
Alors si tu n' as pas inventé : SA' = 3,25 cm
et puisque SA' existe sur le dessin ...
il faut peut-être calculer le volume de cette pyramide S A'B'C'D'
On a déjà dit que k = 3,25/13 = 1/4
Volume de S A'B'C'D' = 192 * (1/4)3
Le volume de SA'B'C'D' je l'ai déjà calculé = 3cm3
sinon je pense que SE = 6.5 cm t'es d'accord ??
et si tu valides j'aurais fini mon exo noté !!!
Bonsoir,
MERCI BEAUCOUP !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
j'ai eu 
grâce à toi
bonne soirée,
à bientôt j'espère !
chatminou
Annuler
connectez vous