Bonjour, tu cherches des tangentes communes et pas le point d'intersection des deux courbes. Tu comprends que ça n'est pas du tout pareil ?
tu sais comment on exprime l'équation d'une tangente en un point x=a d'une courbe y=f(x) ?

L'équation d'un tangente est y= f'(a)(x-a)+f(a) .

Oui tout à fait. Donc le plan ça serait de trouver l'équation d'une tangente à la première courbe en un point a, de trouver l'équation d'une tangente à la seconde courbe en un point b puis de dire que ces deux équations doivent être les mêmes. Autrement dit elles ont mêmes coefficient directeur et même valeur constante.
Cela va te faire deux équations en a et b qui devraient permettre de déterminer a et b

Pourriez-vous donner un exemple avec la première équation, s'il vous plaît ?

Pourquoi tu ne sais pas appliquer y= f'(a)(x-a)+f(a) ?
Si f(x)=-1+x² alors f'(x)=2x et donc f(a)=-1+a² et f'(a)=2a et donc la tangente c'est y=2a(x-a)-1+a²=2ax-a²-1

Mais que faut-il faire avec cette équation ?

ha, tu devrais relire mon post de 16:38 alors.

Je ne sais pas comment faire.

tu as trouvé l'expression de la seconde tangente ?

Il faut commencer par -1+a² ?

Comme j'ai fait pour f tu fais y= g'(a)(x-a)+g(a) ça ne sert à rien de t'avoir montré la première si tu ne sais pas faire la seconde.

Je trouverauis pour la seconde équation:

-x+2a .

Pour y=1/x, y'=-1/x² donc en un point x=b g(b)=1/b et g'(b)=-1/b² et la tangente y=-1/b²(x-b)+1/b=-x/b²+2/b
tu t'es donc encore trompé.

Bon maintenant dit que les deux droites y=2ax-a²-1 et y=-x/b²+2/b sont en fait confondues.

Mais pourquoi ce n'est pas:

x+2b/b  

?

Plutôt:

(x+2b)/b²


?

Et que faire une fois que l'on a dit que les droites étaient confondues ?

"x+2b/b " Pourquoi voudrais-tu que ça vaille ça ? tu as trouvé ça comment ?
Moi je t'ai complètement détaillé le calcul qui donne y=-x/b²+2/b
y=(-x+2b)/b² si tu veux (mais si tu oublies le signe - et que tu oublies aussi les parenthèses et le carré au dénominateur, ça commence à faire beaucoup)

Et donc que faut-il faire après ?

Après avoir dit que les droites étaient confondues.

?

Quelqu'un pourrait m'aider; s'il vous plaît ?

Je te l'ai déjà dit. tu dois dire que les droites y=2ax-a²-1 et y=-x/b²+2/b sont en fait confondues, donc ont même coefficients.
2a=-1/b² et -a²-1=2/b
Avec ça, il faut que tu trouves a et b

On trouve deux couples de valeurs :

Il faut faire un système ?

ben c'est 2a=-1/b² et -a²-1=2/b le système

Bonjour, j'ai le même excercice et je ne comprend pas pourquoi les droites sont confondues

C'est une tangente commune aux deux courbes donc qu'on l'obtienne en faisant y= f'(a)(x-a)+f(a) ou bien y= g'(a)(x-a)+g(a) il faut que ça donne la même droite (sinon elle ne serait pas commune)

merci, mais je n'ai pas non plus compris comment on arrive à "2a=-1/b² et -a²-1=2/b " pouvez vous m'aider?

C'est déjà complètement expliqué dans les posts ci dessus. on a juste calculé y= f'(a)(x-a)+f(a) et y= g'(a)(x-a)+g(a) et égalé les coefficients des deux droites.

je trouve a=-b²/2
en résolvant le système j'obtient: -(-b²/2)²-1=2/b (-b^4)/4=2/b+b/b (-b^4)/4=(2+b)/b
Il y a un problème non?

C'est vrai que l'on trouve des valeurs assez compliquées comme solution du système.

je bloque... Quelles valeurs de a et de b avez-vous trouvé?

Oui c'est très laborieux et je crois même qu'il faut faire des itérations pour trouver les solutions.
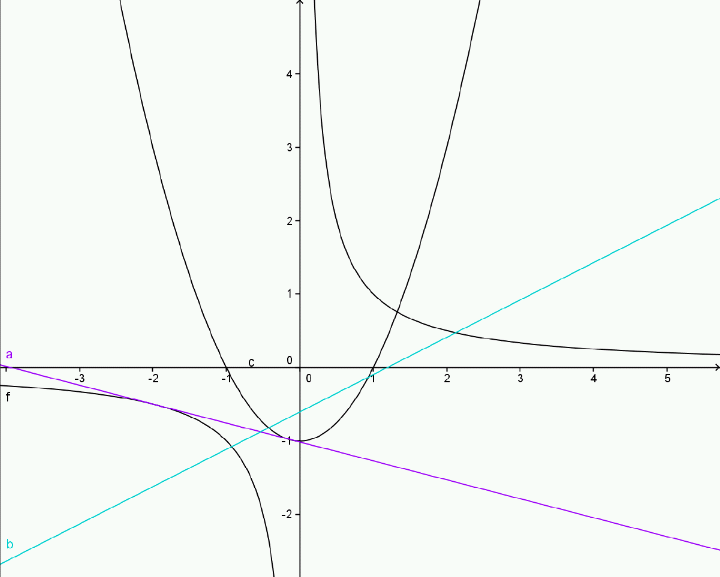
moi j'ai a ~ -0.129209, b ~ -1.96716 et a ~-0.129209, b ~-1.96716
C'est pour ça que j'ai fait un dessin dans geogebra pour me convaincre que ces valeurs n'étaient pas fantaisistes.

Merci beaucoup, en entrant ces données, j'obtient bien la première tangente mais il y a un problème pour la seconde

ha ben oui excuse moi, je t'ai écris deux fois les mêmes, c'est :
a ~ -0.129209, b ~ -1.96716 et a ~ -1.60847, b ~-0.557544

on est bien d'accord que les points de contact c'est A(a,f(a)) B(b,g(b)) A'(a',f(a')) et B'(b,g(b'))