Inscription / Connexion Nouveau Sujet
Calculer l aire !?
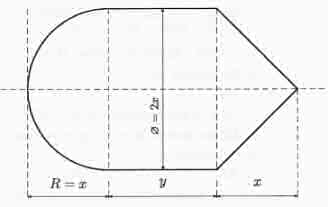
Une bouée (en mer) a la forme ci contre (image en bas) :
Elle est composée d'un cone,d'un cylindre et d'une demi sphère soudées par leurs bases.
1. Calculez en fonction de x l'aire latérale S(x) du solide ainsi que son volume V(x)
2. Calculez les dimensions et la masse de la bouée en répondant aux conditions suivantes :
*volume de la bouée 1m3 ; poids minimal ;
*la bouée est construite en tole d'épaisseur 2mm ; la masse volumique de cette tole est 7.8 kg.dm-3
Je n'y arrive pas.
Pouvez vous m'aider ?
Merci a+
DAM
Je suppose que tu connais les formules les surfaces et volumes d'un cylindre, sphère, cône...
Tu as réussi le 1? Je te fais le cône comme exemple:
avec r le rayon du cône et g la longueur latérale de la base au sommet du cône. Ici r=x et
donc
où h est la hauteur du cône. Ici h=x, donc
Pouvez vous me rappeler les formules.
Je n'ai pas réussi l'exercice 1 ni le 2 !
Aidez moi sil vous plait
Ok, alors pour le cylindre de rayon r et hauteur h on a
et
pour l'aire latérale uniquement.
Pour la sphère de rayon r on a
et
Bonjour,
Je ne m'en sort vraiment pas quelqu'un peut me mettre sur la voie ?
Je ne comprend rien !
Merci.
DAM
Sil vous plait c trop dur j'ai réfléchi toute l'aprèmidi !
Pouvez vous me mettre sur la voie
Comme on veut que le volume de la bouée soit 1, on peut exprimer y en fonction de x: .
Pour l'aire on a on peut remplacer y:
Si maintenant la bouée est creuse et a une épaisseur de 0.002m, la méthode exacte serait de calculer le volume occupé par le matériau le composant, c'est-à-dire V(x+0.002,y)-V(x,y), comme s'il y avait une bouée dans une bouée. Seulement ici je crois qu'on se contente d'une approximation, c'est-à-dire qu'on estime le volume de tôle étant la l'aire multipliée par l'épaisseur. Sous cette hypothèse on aimerait minimiser l'aire:
Ensuite on cherche les extréma de cette fonction:
Je te laisse finir les calculs, il ne reste plus qu'à remplacer le résultat dans les différentes équations. J'espère que tu auras compris cette fois-ci.
Merci :
Seulement une question : A partir du moment ou vous voulez minimiser l'air je n'ai pas compris la démarche et surtout le résultat final !
Pouvez vous m'aider a comprendre ?
Alors je dérive la fonction
puis après j'écirs A'(x)=0 pour trouver les extéma. Ensuite il faudrait vérifier qu'il s'agit bien d'un minimum et non pas d'un maximum... Pour ça soit tu regardes le signe de la dérivée seconde, soit tu fais un dessin, soit tu essaye quelques valeurs.
Bonjour, je ne comprends pas ce que veut dire le 3 au dessus du "V" de  v bizarre mon proffeseur nous en a pas parlé comment on calcue ? Expliquez moi SVP...
v bizarre mon proffeseur nous en a pas parlé comment on calcue ? Expliquez moi SVP...
C'st koi le 3 au desus de la racine carré ?
*** message déplacé ***
Pas de multi-post s'il te plais , un simple "up" fait remonter le topic .
signifie racine cubique de x qui vérifie :
Pareillement :
est la racine quatriéme de x vérifiant :
Et en généralisant :
est la racine n-iéme de x vérifiant :
on note :
la racine 2-iéme ou racine carré de x et la racine 1ére de x est x lui même .

Jord


