Bonjour,

La figure suivante est-elle correcte?



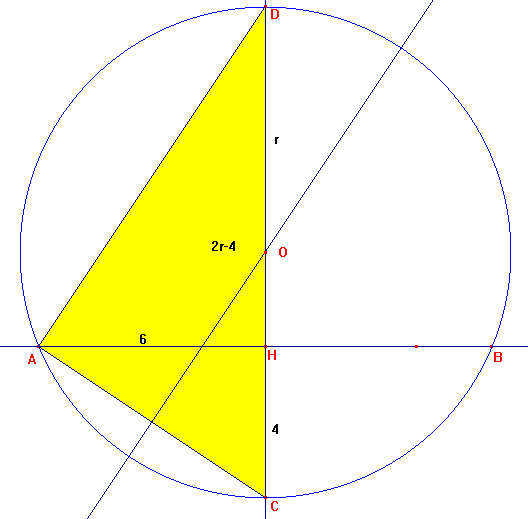
Si oui, dans le tr rectangle CAD le hauteur AH est moyenne proportionnelle entre les 2 segments qu'elle détermine sur l'hypoténuse:

6²=4*(2r-4)=> r=...

Oui cette figure et juste ( le point D a été rajouté).

Donc pourriez-vous m'expliquer comment faire s'il vous plaît ?

Est -ce que l'on doit se servir du théorème de Pythagore ?

Bonjour
si tu fais dans un plan la figure de la face du cylindre sur laquelle se situent A et B
H étant le milieu de [AB], OH est perpendiculaire à [AB]
tu peux le démontrer par le triangle OAB isocèle en O (OA et OB sont deux rayons du cercle)
La médiane OH est donc hauteur.
Par conséquent C est forcément sur (OH) Et compme HC=4cm, C est sur le petit arc AB
et puisque OC=R et HC=4
OH=R-4
et en écrivant Pythagore dans le triangle OHA où AH=AB/2=6cm tu auras
OA²=AH²+HO²
R²=6²+(R-4)²
c'est un équation que tu dois savoir résoudre car les R² s'éliminent et il reste une équation simple du 1er degré.
Et si tu ne trouves pas R=13/2cm c'est que l'un de nous deux se trompe

Oui, c'est bon je trouve la même chose,
donc le rayon du cercle est égale à 13/2
soit 6,5 cm.

Merci beaucoup.

Bonjour à tous
caylus, peux-tu me dire quel site tu as utilisé pour ton dessin. Si c'est Geogebra, je n'ai pas trouvé comment faire des pointillés pour une face cachée dans un solide en perspective. Saurais-tu comment faire ? Merci.

Bonjour Linax, Caylus et Gaa.

On calcule d'abord AC.
AC² = AH²+HC² = 6²+4² = 52.
(HC) étant la médiatrice de [AB], [CD] est un diamètre; d'où l'angle CAD est droit.
cos²(ACD) = CH²/CA² = CA²/CD²;
16/52 = 52/CD²
16CD² = 52*52
CD² = 52*52/16 = 169
CD = 13
Le diamètre est 13 cm et le rayon est 6,5 cm.

Bonjour,  gaa, arrivée à R²=6²+(R-4)² après je ne vois pas trop comment faire les calculs, merci

doit on faire :

R²=6²+(R-4)²
R²= 36+16
R²= 52

?

R²=6²+R²-8R+16
8R=16
R=2