Inscription / Connexion Nouveau Sujet
Calculer un angle dans un parallélogramme
Bonjour,
Je bloque sur une question dans un exercice que je dois faire pour mardi 16/10.
Voici l'énoncé:
Dans un plan muni d'un repère orthonormé (O;i,j) on considère les points A,B et C de coordonnées respectives (-1,1);(4,-3) et (5,5).
1)Placer les points A,B et C dans le plan.
2)Déterminer les coordonnées du point D sachant que le quadrilatère ABCD est un parallélogramme.
3) Déterminer les mesures, en degrés, des angles DAB et ABC du parallélogramme ABCD (on donnera les valeurs arrondies à 10-1).
Voilà, donc la 1) et 2) j'ai réussi mais je bloque sur la 3).
Je ne comprend pas comment on peut calculer un angle dans cette situation sans avoir d'autres angles avec les degrés donnés.
J'ai regarder toutes les propriétés d'un parallélogramme avec les angles opposés, etc...
Mais la franchement, je ne sais pas.
Sa serait sympa si vous pouviez me répondre ce soir ou demain. Merci
PS: Voici le graphique:
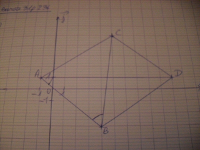
Oui, j'ai vu le produit scalaire, est-ce que c'est cela qu'il faut faire ?:
AB=V(4+1)²+(-3-1)²=V41=6,4
DA=V(-1-10)²+(1-1)²=V121=11
DA.AB=(10*(-1))+(1*(-3))=-13
vectDA.vectAB=DA*AB*cos(DA,AB)
-13=11*6,4*cos(DA,AB)
-13=70,4*cos(DA,AB)
cos(DA,AB)=-13/70,4=-0,18
cos(-0,18)=0,99°
Sauf que j'au dû me tromper quelque part car je pense que l'angle doit être au tour de 50°...
DA.AB=(10*(-1))+(-1*4)+(1*1)+(1*(-3))
=-10-4+1-3
=-16
Es-ce que c'est cela ? Je n'ai pas bien compris la formule...
Ah non c'est bon j'ai compris la formule désolé :/
Donc c'est:
(-10*5)+(0*(-4))
=-50
mais sa me donne: -50/70,4=-0,71
donc: Arccos(-0,71)=135,2°
Je trouve que cela fait beaucoup 

 jai reussi
jai reussi
