Inscription / Connexion Nouveau Sujet
Centre de symétrie d'une fonction
Bonjours à tous.
Je rencontre un problème dans mon exercice concernant le centre de symétrie d'une fonction car je n'ai jamais abordé le centre de symétrie, mais seulement l'axe.
Voici l'énoncé:
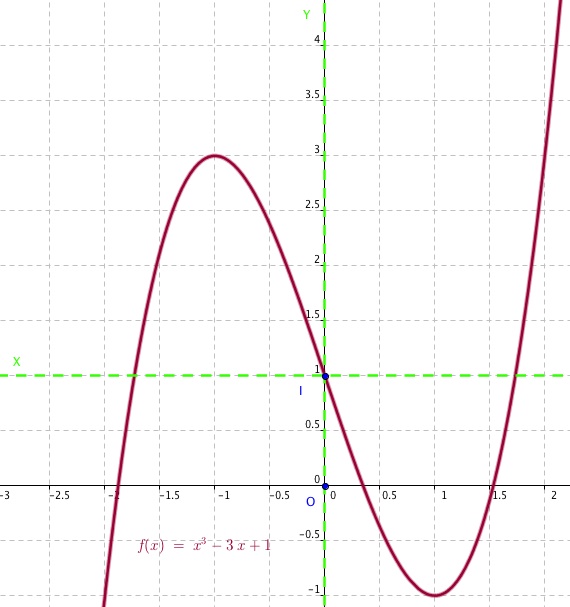
Soit f(x)=x3-3x+1
Montrer que I(0;1) est centre de symétrie de Cf.
Merci aux personnes qui pourront m'apporter une aide.
Bonjour,
Il te faut faire un changement de repère de en
et montrer que ta nouvelle fonction
est impaire dans ce nouveau repère.
On ne "calcule" par une parité ...
Met toi dans le repère (I,X,Y) en vers ci-dessus, donc I pour origine (et non plus O) et les axes X et Y (et non plus x et y)
Tu vois bien que dans ce nouveau repère, ta fonction est impaire.
Or, une fonction impaire admet l'origine (donc ici I) comme point de symétrie.
Merci beaucoup! J'ai trouvé une formule me permettant de calculer le centre de symétrie de la fonction: I(a,b) est centre de symétrie si f(a+x)+f(a-x)=2b.
Supposons que tu sois Ok.
Donc
X=x ==> x=X
et
Y=y-1 ==> y=Y+1
Tu as
Donc
Donc
D'où
et donc
On a
La fonction f est donc bien impaire dans ce nouveau repère (I,X,Y), elle admet donc I comme centre de symétrie.
D'accord. Donc quand la fonction est impaire, il y a obligatoirement un centre de symétrie. Mais comment démontrer que c'est le point I?