Inscription / Connexion Nouveau Sujet
Coefficient directeur.
Bonjour ,
Merci d'avance. 
(C) est la courbe représentative de la fonction f définie sur ]0;+∞[ par .
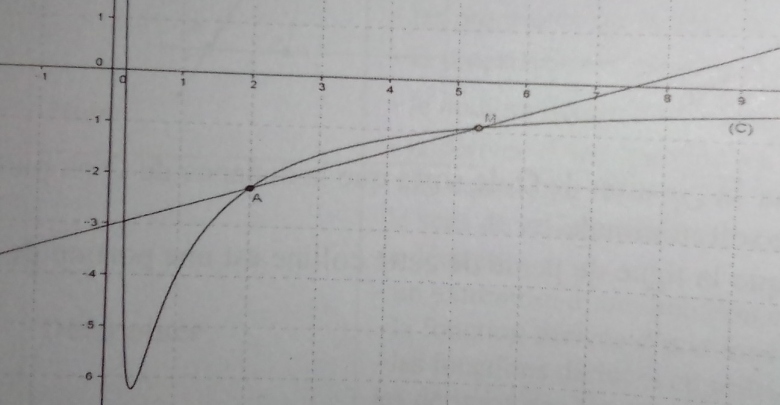
A est le point de (C) d'abscisse 2 et M est un point de (C) distinct de A et d'abscisse .
1) On note le coefficient directeur de la droite (AM).
Calculer .
2) Démontrer qu'une équation de la droite (D) passant par A et de coefficient directeur est :
.
Tracer (D).
Réponses
1) .
2) Je n'arrive pas à faire
Bonjour
revoir la réponse à la 1)
si tu prends la lim à gauche , tu dois prendre la limite à droite
et tu dois réellement chercher cette limite
Bonjour,
Tu peux calculer les coordonnées de A, puisqu'un point appartenant à une courbe dont tu as l'équation a toujours pour coordonnées A(x;f(x)).
Je suis d'accord pour les coordonnées de A, mais pour M, tu ne peux pas donner de valeur numérique, puisque son abscisse est une variable x.
Ciramor, bonjour
je te remercie de prendre connaissance de ![]() Sujet ancien- ne plus donner ce lien-merci
Sujet ancien- ne plus donner ce lien-merci

Pour la question 1, tu commence donc avec:
, après tu simplifie au maximum les fractions.
Normalement, tu tomberas sur
A partir de là, tu peux factoriser le numérateur et tu vas remarquer quelque chose
Donc .
2) On a A(2;-9/4) ==> .
La droite d'équation a pour coefficient directeur 1. Cette droite passe donc par A(2;-9/4).
Par conséquent une équation de la droite (D) passant par A et de coefficient directeur est :
.
Pour la construction , on donne une valeur quelconque à pour trouver
.
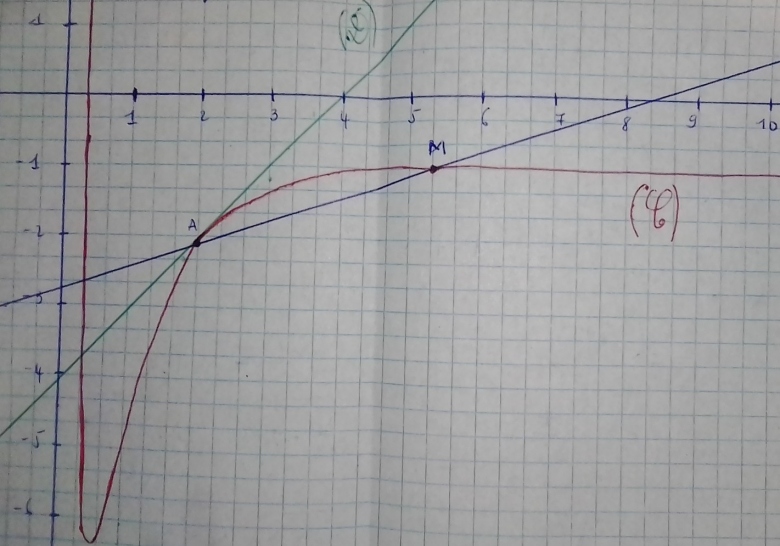
Ce passage est faux
La droite d'équation
Donc si je comprends bien , à l'instar du passage en rouge , tout le reste aussi est faux pour cette question ..
ben si tu mets un "donc" qui est faux, le raisonnement tombe à terre,...et la question reste à traiter
OK
Donc
2) On a A(2;-9/4) ==>
La droite d'équation
Par conséquent une équation de la droite (D) passant par A et de coefficient directeur
Pour la construction , on donne une valeur quelconque à

Donc
2) On a A(2;-9/4) ==>
La droite d'équation
Par conséquent une équation de la droite (D) passant par A et de coefficient directeur
.....
Si le couple de coordonnées du point A est différent de (2;-9/4) alors et donc
La droite d'équation a pour coefficient directeur 1.
Non ?
Si le couple de coordonnées du point A est différent de (2;-9/4) alors
La droite d'équation
Non ? et alors ? tu n'as toujours pas répondu pour autant, tu nous amuses là...
2) On a : .
Le coefficient directeur de (D) est 1.
(D) passe par A si et seulement si les coordonnées de A vérifient l'équation de (D).
.
A(2;-9/4)
.
Donc les coordonnées de A vérifient l'équation de la droite (D).
D'où (D) passe par le point A.
Et on a montré que l=1.
Par conséquent une équation de la droite (D) passant par A et de coefficient directeur l est : .
la partie rédigée avec l'équivalence, je n'aurais pas nécessairement rédigé ainsi, mais oui, cette fois le raisonnement est juste



