Inscription / Connexion Nouveau Sujet
Comment démontrer que 3 points sont alignés DM
Exercice 1
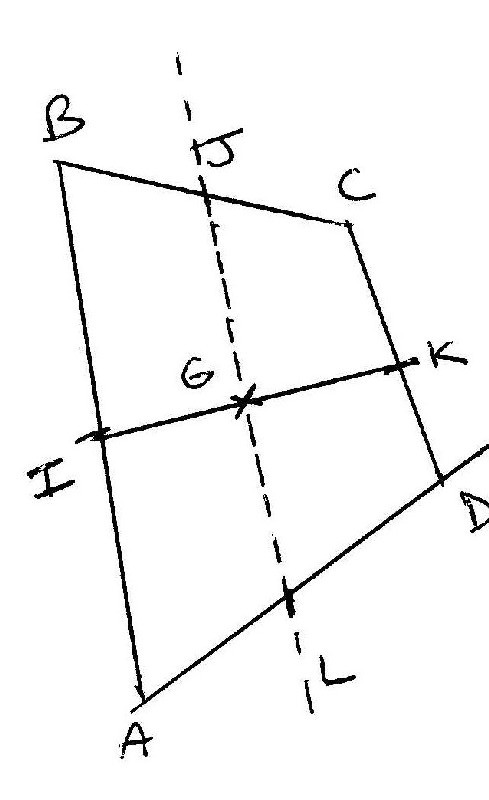
On se donne un quadrilatère quelconques ABCD , et on construit les points suivants:
I milieu de [AB]
J milieu de [CB]
K milieu de [CD]
L mIlieu de [AD]
G Milieu de de [IK]
1) Fait le dessin ( Voir figure )
2) Montrer que les points G , J et L sont alignés
On sait que I milieu de [AB] donc I est l'isobarycentre de [AB]
Donc IA = 1/2 AB
Idem pour les points J K L G
JB = 1/2 BC KC = 1/2 CD LD = 1/2 DA GK = 1/2 KI
Ou par colinéarité mais je sais pas comment faire
Je vois pas par ou je peux partir pour démontrer que les points G J et L sont alignés j'ai mis toutes mes pistes de réflexion
Merci de votre aide
Voici une méthode que tu peux essayer :
Tu calcules, par décomposition vectorielle selon la règle de Chasles, GJ en passant par I, puis par K. Idem pour GL.
Puis tu additionnes les quatre égalités oobtenues.
Tu verras ce que ça donne.
Bonjour,
Je te donne une autre piste avec les barycentres:
G bar (I;2) (J;2) car milieu
G bar (A;1)(B;1) (C:1)(D;1) Théorème du barycentre partiel
G bar (A;1)(C;1) (B;1)(D;1)
...
je te laisse finir

Je sais pas pourquoi tu veux passer par GJ en passant par I, puis par K. Idem pour GL.
Puisque On sais pas que G est le milieu de [JL] on sais rien
Donc on ne peux faire ta méthode
On m'a dit sinon de procédé par colinéarité mais j'arrive pas a le faire dans ce cas
Bonjour,
Autre méthode : tu exprimes G comme barycentre de J et L (en utilisant l'associativité du barycentre).
@ Pour sariette
Si G est le barycentre de [IK] et pas de [IJ]
( Le trait c'est pour vous montrer se que dois démontrer :s )
Si G est le barycentre de [IK] et pas de [IJ] donc
G est l'isobarycentre de ( I , 1 ) et ( K , 1 )
Puisque G milieu de [IK]
G = 1/2 [KI]
Et je ne te suis pas pour le théoreme partiel , Je pense que je ne l'ai pas appris
Je suis partit dans les barycentres mais je ne sais pas ci cela vas me mener quelques parts
Donc on G barycentre de ( I ; 1 ) ( K ; 2 )
GI + GK = 0
I barycentre de ( B ; 1 ) ( A ; 1 )
IA + IB = 0
K barycentre de ( C ; 1 ) ( D; 1 )
KC + KD = 0
J barycentre de ( B ; 1 ) ( C ; 1 )
JB + JC = 0
L barycentre de ( A ; 1 ) ( D ; 1 )
On peux dire cela puisque les points sont des milieux de segment et donc sont tous des isobarycentres de ses segments puis apres
J'ai essayé d'associé des barycentres entre eux mais en fin
par exemple : K barycentre de ( C ; 1 ) ( D; 1 )
KC + KD = 0
J barycentre de ( B ; 1 ) ( C ; 1 )
JB + JC = 0
Donc par associativité on a
KC + KD = 0
( on introduit le point J ) ce qui nous donne
KJ + JC + KJ + JC = 0
et la je sais pas comment faire . . . Je suis bloqué
Et sinon par colinéarité J'arrive pas
Puisque si les vecteurs sont colinéaire alors les points sont alignés mais je ne sais pas par ou comméncé pour cela
merci de votre aides , Je tourne en rond depuis deux heures :s
oui sur mon brouillon il y avait aussi IK au lieu de IJ mais j'ai tapé trop vite ! :S
le théorème du barycentre partiel dit que l'on peut remplacer un système (A;a) (B;b) par son barycentre G avec le coefficient (a+b) c'est à dire par (G;a+b) ( on peut faire ce remplacement dans les deux sens. Si on a (G;a+b) on peut mettre à la place (A;a) (B;b))
je finis donc ma démo en espérant ne pas me retromper avec les points:
G milieu de [IK]
<=> G barycentre de (I;2)(K;2) je peux mettre 2 et 2 comme coef au lieu de 1 et 1
<=> G barycentre de (A;1)(B;1) (C;1)(D;1) ici j'ai remplacé (I;1+1) par (A;1) et (B;1)
<=> G barycentre de (A;1)(D;1) (B;1)(C;1) ici j'ai juste changé de place les couples
<=> G barycentre de (L;2) (J;2) (car L isobarycentre de A et D et J isobarycentre de B et C)
=> G, L et J sont alignés
Si tu n'as jamais vu cette propriété, passe par la méthode de Priam

Merci sariette mais pour la méthode de Priam je ne l'est pas comprise :s
Donc si j'ai compris ton raisonnement :
Ta utilisé la propriété d'associativité
+ le théoreme
G milieu de [IK]
G barycentre de (I;2)(K;2) au lieu de mettre 1 tu met 2 donc cela ne change pas et puisque G milieu de [IK]
=> La je suis d'accord avec toi
G barycentre de (A;1)(B;1) (C;1)(D;1) ici j'ai remplacé (I;1+1) par (A;1) et (B;1)
=> Ici grâce a la propriété d'associativité ( I : 2 ) = ( A ; 1 ) + ( B ; 1) et pareil pour le point K ,
=> Je suis d'accord la
<=> La Comme I barycentre de ( A : 2 ) et ( B : 2 ) et K Barycentre de ( C ; 2 ) ( D ; 2)
==> Je t'ai pas suivi la puisque tu dis que ta remplacé ( I ; 2 ) par ( A ; 1) et ( B : 1 ) un peu plus haut donc I barycentre de ( A ; 1) et ( B : 1 ) sauf si ta fais comme G car I milieu de [AB]
<=> G barycentre de (A;1)(D;1) (B;1)(C;1) ici j'ai juste changé de place les couples donc divisé par 2
==> J'ai pas compris pourquoi ta changé de place les couples enfin est ce que cela change quelques chose
<=> G barycentre de (L;2) (J;2) (car L isobarycentre de A et D et J isobarycentre de B et C)
=> G, L et J sont alignés
Excuse moi après réflexion et analyse du sujet !
enfete c'est moi qui me suis embrouillé avec les points merci encore !
Si j'ai un problème je le poste
mais merci encore ! Je pensé pas utilisé l'associative comme ceci
Merci
<=> G barycentre de (A;1)(D;1) (B;1)(C;1) ici j'ai juste changé de place les couples
==> Changé les places des couples cela change t-il quelques chose ?
non bien sûr que ça ne change rien !
C'est peu comme dire
Jules est le frère de Marie, Pierre et Jacques
ou bien Jules est le frère de Jacques, Marie et Pierre ...
Je reviens sur ma méthode qui, sauf erreur, paraît bien fonctionner :
GJ = GI + IB + BJ
GJ = GK + KC + CJ
GL = GK + XD + DL
GL = GI + IA + AL
J'additionne tout :
2(GJ + GL) = 2(GI + GK) + (IB + IA) + (KC + KD) + (BJ + CJ) + (DL + AL).
Au second membre, tous les termes entre parenthèses sont nuls. D'où GJ + GL = 0.
Evidemment, elle est moins noble qu'une méthode barycentrique.....
et pour te montrer que la méthode de Priam marchait très bien:
en vecteurs:
GI = GJ + JB + BI
GI = GL + LA + AI
GK = GJ + JC + CK
GK = GL + LD + DK
on ajoute les 4 membre à membre
2(GI + GK) = 2(GJ+GL) + (JB+JC) + ((LA+LD) + (AI+BI) + (CK+D)
les sommes de droites sont toutes nulles car elles font intervenir les points et leurs milieu.
Donc GI + GK = 0 et donc GI + GK = 0 ce qui montre que G est le milieu de [IK} et donc les points sont alignés...

Je te suis très reconnaissant ! Merci beaucoup je serais dans la caca si tu étais pas la 
Merci beaucoup pour cette aide précieuse et repose toi bien et guérie vite 
merci pour tes vœux!
Jette quand même un œil à la méthode des vecteurs qui a l'immense avantage d'être simple à comprendre et courte!

La méthode de Priam je la comprend pas du tout 
Enfin je comprend ce qu'il fait mais apres je met perd dans le regroupement des membres :
2(GI + GK) = 2(GJ+GL) + (JB+JC) + ((LA+LD) + (AI+BI) + (CK+D)
avec la méthode de Priam donc on a
en vecteurs:
GI = GJ + JB + BI
GI = GL + LA + AI
GK = GJ + JC + CK
GK = GL + LD + DK
on ajoute les 4 membre à membre
2(GI + GK) = 2(GJ+GL) + (JB+JC) + ((LA+LD) + (AI+BI) + (CK+D)
JB + JC = J barycentre de ( B ; 1) ( C ; 1 )
J Milieu de [BC]
LA + LD = L barycentre de ( A ; 1) ( D ; 1 )
L Milieu de [DA]
AI + BI = I barycentre de ( A ; 1) ( B ; 1 )
I Milieu de [AB]
CK + KD = K barycentre de ( C ; 1) ( D ; 1 )
K Milieu de [CD]
2(GI + GK) = 2(GJ+GL)=> Je sais pas a quoi ca me sert :s
Mais non... laisse tomber les barycentre ici !
On travaille en vecteurs.
JB+JC= 0 car J milieu de [BC]
AI +BI = 0 car I milieu de [AB]
etc..
donc au final : 2(GI + GK) = 0 c'est à dire GI + GK = 0 et donc G est le milieu de [IK]
tu vois?
Non mais ca je suis d'accord mais moi faut que je demontre que L , G et L sont alignés :s
Et pour la rédaction je galere un peu :s
ah oui j'ai encore écrit de traviole :S j'ai mélangé hypotheses et conclusion parce que mon dessin est à l'envers du tien.Il est temps que j'aille me coucher...
mais Priam avait bien écrit ses vecteurs !!
je renonce à tout recommencer, relis ce qu'il a écrit à 17h15 en suivant l'idée que je t'ai expliquée ensuite en me trompant de vecteurs 
Les sommes sont nulles car chaque fois le point est milieu des deux autres.
tu vas comprendre...
--------
pour Priam>>
Il n'y a aucun jugement de valeur entre les méthodes ! 
Ce qui est intéressant justement c'est de montrer différentes façons d'arriver à un résultat.
J' espère que tu n'as pas été froissé par mon intervention ...

Je voulais te remercier pour avoir pris du temps pour m'expliquer le DM
et les pistes réflexion pour hier et desolé d'avoir pris ce temps sur tes autres activité
MErci pour le DM cetais bien cela et pour l'histoire des VEcteurs je l'ai refais avec les bons vecteurs et ca marche juste remplacé les mauvaises lettres par les bonnes



