Bonjour,

il te reste à calculer les limites en +oo et -oo

oui mais comment ? Je n'ai pas vu les limites en cours ?

Merci

Tu n'as pas vu les limites !!

Alors je ne vois pas trop comment répondre ...

Ah si, tu peux aussi étudier le signe de la fonction f à l'aide d'un tableau.

Ok, donc

- pour x²-6x+10, delta < 0 donc pas de solutions.

- pour 2x-6, soit x = 3

*

en quoi je peux dire que c'est borné en 1et -1 ? Parce que là je voie pas trop ...

Au fait quand je dis que je n'ai pas vu les limites, j'ai juste vu :

et on fait tendre h vers 0

Sur l'intervalle [4;+oo[ la fonction est décroisante et positive, et le maximum vaut 1, donc ...

ok, donc je dis :

- sur l'intervalle [4;+00[ f est décroissante et positive, et le maximum vaut 1, donc, 1 est un extremum local de f

- sur l'intervalle ]-00;2] f est  décroissante et négative, et le minimum est -1, donc, -1 est un minimum local de f

Pour conclure, f admet un minimum et un maximum, ainsi on peut dire que f est bornée en 1 et en -1

C'est bon ?
Merci pour ton aide Jamo :)

Non, pas exactement.

Sur l'intervalle [4;+oo[ la fonction est décroisante et positive, et le maximum vaut 1, donc f(x) est compris dans l'intervalle [0;1] sur [4;+oo[

A peu prés la même chose sur ]-oo;2] : f(x) compris dans [-1;0]

Et pour x dans [2;4], f(x) est compris dans [-1;1]

ok, mais je ne voie pas en quoi elle est bornée sur 1 et -1...

Au fait, quand la fonction est bornée, c'est bien quelle est admet un minimum local en -1 et une maximum local en 1 ?

Un fonction bornée par -1 et 1, ça vaut dire que pour tout x, on a : -1 <= f(x) <= 1

ok, donc si je suis ton raisonnement de 19:54, c'est bien démontré ?

Merci pour ton aide Jamo

Essaie plutot de comprendre ce qui se passe.

Regarde l'image ci-dessous, c'est la représentation graphique de la fonction f.

Etre borné par -1 et 1, ça veut dire que tu peux "enfermer" la courbe entre les droites horizontales d'équation y=1 et y=-1.

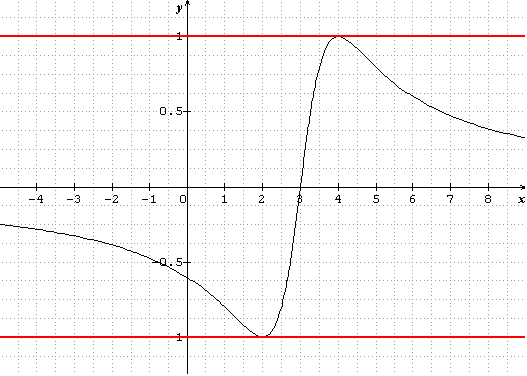
Maintenant, avec cette courbe, le tableau de variations de ta fonction f et son tableau de signe, je pense que tu peux comprendre comment on justifie que la fonction est bien bornée par -1 et 1.

ok, merci beaucoup Jamo

Bonjour
autre méthode : pour tout x réel. analogue pour montrer que pour tout x,

Merci pour ta réponse Lafol , mais c'est bon aussi ce que l'on a a fait avec Jamo plus haut ?  

perso je pense comme lafol
c'est bcp plus simple de calculer f(x)- (-1) et de trouver le signe
et idem avec f(x)- 1


toutefois ce que vous avez fait avec jamo est bon qd même

Non, car vous n'avez pas prouvé que f ne redescend pas sous -1 quand x > 4, ni qu'elle ne remonte pas au dessus de 1 pour x < 2.... et tant que tu n'as pas vu les limites, tu ne peux pas le faire ....

si, il y avait le tableau de signe tout en haut ! donc f ne dépasse pas 0 avant x=2 etc ...
c'était bon aussi, du coup

bin si elle est positive forcément elle peut pas descendre sous -1


^{salut au fait ..}

Alors, j'avoue que je suis un peu désorientée.....c'est bon ou pas ? Voici ce que j'ai faiS exactement :

(j'ai faiS le tableau de signe de f est ses variations avant) :

- Sur l'intervalle [4;+oo[, la fonction est décroissante et positive, et le maximum vaut 1, donc f(x) est compris dans l'intervalle [0;1] sur [4;+oo[

- Sur l'intervalle ]-oo;2], la fonction est décroissante et néative, et le minimumu vaut -1, donc f(x) est compris dans l'intervalle [-1:0]

- Sur l'intervalle [2;4], la fonction est croissante et f(x) est compris dans [-1:1]

Ainsi, on peut en déduire que f est bornée par -1 et 1, car, pour tout x, on a : -1 f(x) 1.

Voilà, est ce que c'est bon expliqué comme ceci ??

Merci à vous deux

:)

Oui, c'est bon.

oui ça m'a l'air pas mal
très compliqué mais bien

regarde comment j'aurais fais

f(x)-1= (2x-6-x²+6x-10)/(x²-6x+10) alors en bas le delta est <0 donc c'est positif (du signe de a)
en haut ça fait -x²+8x-16 = -(x-4)² donc négatif
donc f(x)-1 <0 toujours donc f(x)<1 et hop 2 lignes et c fini
  idem pour l'autre

ok, re-merci à vous deux

Sinon, j'ai du mal, à dicerner :

non non c bon
c'est juste
tout va bien ...

Ok, merci alors, tu me rassures (j'avais pas envie de recommencer ma copie)