Inscription / Connexion Nouveau Sujet
Comment tracer la courbe f à partir de la courbe de sa dérivée?
Bonjour,
J'ai un exercice à résoudre et je dois répondre par vrai ou faux à des affirmations proposées. Peu importe ici n'est pas le probleme.
En fait, sur mon énoncé j'ai une courbe C qui représente la fonction dérivée f' , définie sur I=[0 ; 4].
Et je dois (je pense) réussir à tracer la courbe représentant la fonction f afin de pouvoir répondre à mes questions de l'énoncé.
Mon probleme et que je ne sais plus (pas?) comment faire pour tracer la courbe de la fonction f à partir de la courbe de la fonction dérivée f'.
Un peu d'aide serait bienvenue  J'ai chercher sur le net et j'ai trouvé pas mal d'exercices expliquant comment tracer f' à partir de f mais pas l'inverse et j'avoue etre un peu perdue...
J'ai chercher sur le net et j'ai trouvé pas mal d'exercices expliquant comment tracer f' à partir de f mais pas l'inverse et j'avoue etre un peu perdue...
Info supplémentaires:
- f est définie et dérivable sur l'intervalle I=[0 : 4]
- On sait que f(4)=0
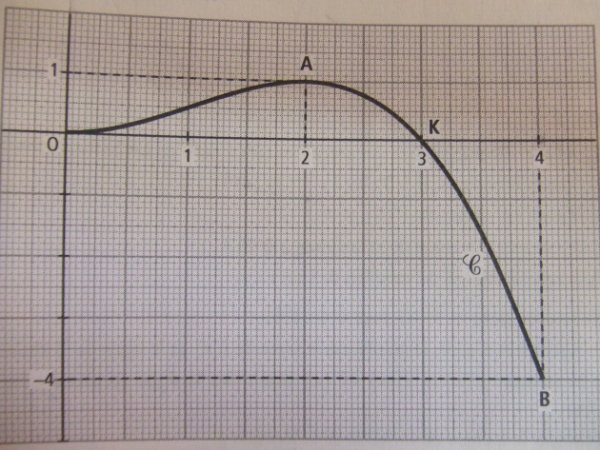
- Les points A(2 ; 1), K(3 ; 0) et B(4 ; -4) sont situés sur la courbe C.
Merci d'avance 
Bonjour
La fonction f ' étant donnée, il existe une infinité de fonctions f qui ont pour dérivée f'.
Il serait utile de donner l'énoncé complet.
Bonjour . Tu n'as pas d'autre renseignement pour f(x) ?...à part f(4)=0 ?...
Trace déja le point de f(x) sur ton repère : M(0; 4) puisque f(4) = 0 .
En ce point , la dérivée f(4)' = - 4 (point B).
Donc la tangente en M vaut -4 : en M tu traces une petite tangente de pente - 4.
Maintenant, un peu à l'aventure ...
Pour x=3 , on va supposer que f(3) = 3 ... par exemple. avec une tangente horizontale, puisque f(3)' = 0
Pour x=2, on suppose que f(2) = 2 ... peut-être, avec une tangente de coefficient directeur (pente) +1 puisque f(2)' = 1
Tu pourras rajouter d'autres points, si tu as des valeurs pour f(x)'.
Non Rene38, je n'ai pas d'autres info. Je vous remet l'énoncé au complet comme sur mon livre :
Répondre par vrai ou faux, sans justification, a chacune des huits affirmations proposées.
Soit f une fonction définie et dérivable sur l'intervalle I=[0 ; 4].
On sait de plus que:
- f(4)=0
- La courbe C représente la fonction dérivée f ' de la fonction f, définie sur I=[0 ; 4].
- Les points A(2 ; 1], K(3 ; 0) et B(4 ; -4) sont situés sur la courbe C.
Ensuite j'ai donc ma courbe de f ' de dessinée (dsl je ne peux pas vous la mettre sur l'ordi) Mais en gros elle est croissante sur [0 : 2] puis décroissante sur [2 ; 4].
Ensuite voici les affirmations proposées :
1) La fonction f est croissante sur l'intervalle [0 ; 3].
2) La fonction f est maximale pour x=2.
3) La fonction f est maximale pour x=3.
4) La fonction f est décroissante sur l'intervalle [2 ; 4].
5) On a f(3,5)<0.
6) La tangente a la courbe représentative de la fonction f au point d'abscisse 2 est parallele a l'axe des abscisses.
7) On a f(2) f(3).
f(3).
8) La tangente a la courbe représentative de la fonction f au point d'abscisse 4 a pour équation y=-4(x-4).
Pour répondre a ces 8 affirmations proposées, j'ai pensé qu'il fallait tracer la courbe f ...
Je vais essayer de faire comme la suggéré jacqlouis.
Si vous avez d'autres idées avec les nouveaux éléments que j'ai mis, n'hésitez pas car je suis toujours un peu perdue 
Je suis vraiment désolée, c'est vrai que j'aurai du tout mettre du premier coup 
Ce n'est pas grave si vous n'avez pas le temps tout de suite, je serais la vers 17h donc si je vois que vous etes venu voir mon sujet...
Bonjour,
La courbe C tu pourrais nous l'envoyer en respectant : Pour savoir comment envoyer une image et quelles images sont tolérées ici , il suffit de lire la FAQ = Foire Aux Questions ici : 
![]() [lien]
[lien]
Lire la réponse à la question 05 .
Et pour nous envoyer une image, 2 solutions :
- tu scanes le schéma (rien que le schéma)
- tu reproduis le schéma avec un logiciel comme Paint ou un logiciel de dessin géométrique ( Géogébra , SineQuaNOn etc ....)
En déterminant sur quels intervalles f '(x) est > 0 ou > 0 , tu peux aussi déduire si la fonction f est croissante ou décroissante sur tel ou tel intervalle !
D'accord merci Bourricot !
Je vais essayer de continuer l'exercice et je vous mettrais ce que j'ai trouvé plus tard si ca ne vous dérange pas ...
Bien sur j'essayerai aussi de joindre la courbe pour que vous puisiez y voir plus clair !
Il faudrait la courbe C.
Mais avec les infos données, on peut déjà répondre à presque toutes les questions.
2) faux car f '(x) > 0 à gauche et à droite de l'abscisse 2.
3) Il a un maximum local de f(x) pour x = 3 car f '(x) > 0 à gauche de 3, f '(3) = 0 et f '(x) est négative à droite de 3.
4) faux, elle est croissante sur [2 ; 3] puisque dans cet intervalle, f '(x) > 0
5) faux, car f est décroissante sur [3 ; 4] puisque f'(x) < 0 sur cet intervalle et donc f(3,5) > f(4), soit f(3,5) > 0
6) faux, car f '(2) est différent de 0.
7) faux, car f '(x) > 0 sur [2 ; 3] et donc f(x) est croissante dans cete intervalle --> f(2) < f(3)
8) vrai, car (4 ; 0) est bien un point de la courbe représentant f(x) et f '(4) = -4
-----
Sauf distraction (rien relu). 
Voici la courbe C, je n'ai pas réussis a la scanner alors j'ai pris une photo avec mon appareil, j'espere que ca ira