Inscription / Connexion Nouveau Sujet
Comparaison de probabilité
Bonjour,
Je tente d'aider mon fils sur un exo de proba, mais mes notions sont fort fort lointaines...Voici l'énoncé :
Une urne opaque contient 2 billes numérotées 1 et n billes numérotées n (n est un nombre entier naturel non nul).
On prélève au hazard et avec remise 2 billes de cette urne et on note les numéros obtenus.
a. On considère:
A: « Le produit des numéros obtenus est égal à n »;
B: « La somme des numéros obtenus est égale à 2 ».
Pour quelle valeur de n a-t-on P(A)=10 P(B) ?
Merci pour votre aide - Pleeeaaaase Heeeelp 🙏🏻💪
Bonjour,
je pense qu'il faut commencer par faire un arbre
Et j'imagine que n n'est pas égal à 1 (sinon toutes les probas vaudront 1)
Bonjour,
Vous pouvez commencer par calculer P(A), P(B) et P(A)/P(B) pour n=1,2 et 3, avec des arbres de probabilité. Ça peut vous inspirer pour trouver des expressions de P(A) et P(B) en fonction de n.
n peut aussi être égal à 1, en effet toutes les probabilités vaudront 1 dans ce cas.
Ce qui complique la tache, c'est qu'il y a 3 fois plus de chances de tirer une bille portant le numéro 1 qu'une autre bille 🤯
Comment ça ?
Si n=2, il y a 2 billes numérotées 1 et 2 billes numérotées 2. Quelle est la probabilité de tirer une bille numérotée 1 ?
Je n'avais effectivement pas compris le pb comme cela ...
Je pensais à 2 boules n°1 et 1boule n°1, une boule n°2, une boule n°3 ...
Non, n est un paramètre du problème.
Si n=5, il y a 2 boules numérotées 1 et 5 boules numérotées 5 dans l'urne, et rien d'autre.
Avez-vous fait l'arbre des probabilités pour n=2 ?
Lorsque j'étais à l'école, on faisait directement les calculs, je ne sais pas à quoi correspond un arbre...😢
Donc P(A) correspond à la probabilité de tirer une boule N°1;
Pour n=1 —> 1
Pour n=2 —> 1/2
Pour n=3 —> 2/5
Pour n=4 —> 1/3 ...
L'événement A c'est "le produit des numéros des deux billes tirées est égal à n".
Pour n=2, le produit doit être égal à 2, donc il faut tirer une boule n°1 et une boule n°2 : 1*2=2
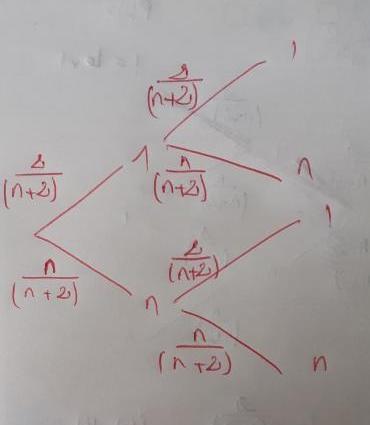
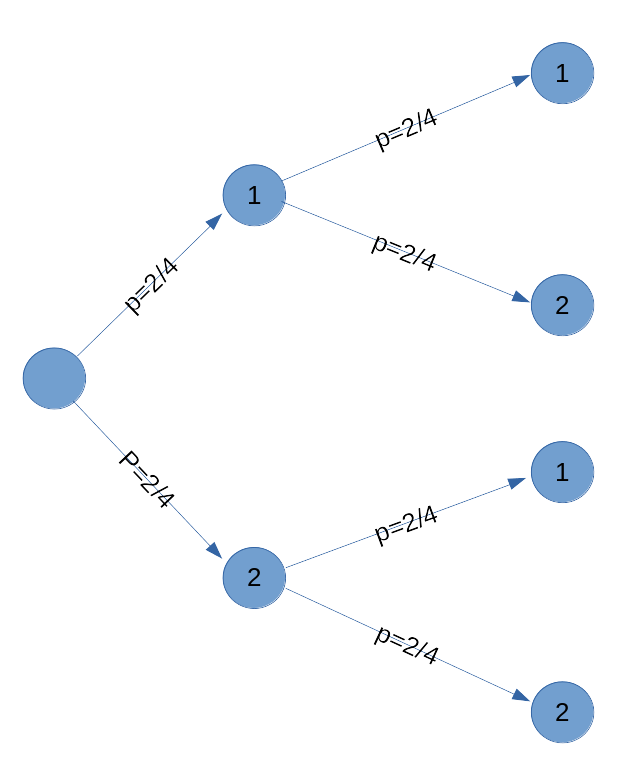
Ci-dessous l'arbre pour n=2.
On voit que la probabilité d'avoir une boule n°1 et une boule n°2 est :
Bonjour, j'ai lu toutes mes réponses et j'arrive pas a trouvé P(A) et P(B) en fonction de n.
Besoin d'aide.
Bonjour,
Ci-dessus, j'avais fait l'arbre pour n=2. Si tu as compris cet arbre, tu peux l'adapter pour n quelconque.
C'est ce que j'ai fait et j'ai trouver P(A)=2/(2+n) mais je n'arrive pas à trouver P(B)

Il manque des parenthèses pour en être sûr, mais ça y ressemble, oui.
Et après simplification ?
Et P(B) maintenant ?
P(A) = 4n/(2+n)2
Et pour P(B) je pense à faire le seul chemin qui peut faire 2 et donc P(B)= 2/(2+n)*2/(2+n)
OK pour P(A).
P(B) a l'air bon aussi, reste à simplifier et à conclure.
Attention au cas spécifique n=1, les formules ne fonctionne pas dans ce cas, il faut le traiter séparément.
P(B) = 4/(2+n)2
Et pour répondre à la question P(A)=10×P(B) il faut donc résoudre l'équation 4n/(2+n)2 = [4/(2+n)2] *10
Je trouve n=10
C'est juste.
Il reste le cas n=1 à vérifier séparément, vu que les formules ne fonctionnent pas dans ce cas-là. Pas besoin de formules pour n=1, on peut calculer les probabilités directement en fractions numériques.
Ok merci beaucoup.
Dans cet exercice, il ya a une deuxième question :
C=" le produit des numéros obtenus est égal a n2"
D=" la somme des numéros obtenus est egal n +1"
Pour quelle valeur de n a-t-on P(C)=5P(D)
Je vais essayer de le faire seul et est ce que je pourrais vous envoyer les réponses pour que vous vérifier.
Je trouve P(C) =n/(2+n)2*n/(2+n)2 = n2/(x+2)2
P(D)=4n/(2+n)2
Je résous l'équation
n2/(n+2)2 = 4n/(n+2)2 *5
Je trouve 20
Je trouve P(C) =n/(2+n)2*n/(2+n)2 = n2/(x+2)2
P(D)=4n/(2+n)2
Je résous l'équation
n2/(n+2)2 = 4n/(n+2)2 *5
Je trouve n= 20