bonjour;
tu connais les limites pour les fonctions.
1/x    en plus et moins l'infinie c'est 0

et bien c'est ca mais pour une suite.

exemple

u(n) = 1/n

converge vers 0
c'est tout, c'est une limite de suite. Attention cette limite doit étre un réel pour parler de convergence.

Tu t'en fiches de la définition d'une suite telle qu'elle est donnée dans le programme... Je comprenais pas en premiere/term celle qu'ils nous donnaient et ça m'a pas empêché de m'en sortir

Faut te dire que c'est comme les fonctions mais en l'infini

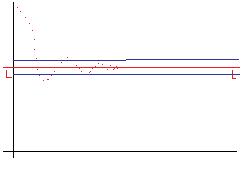
pour un shema

je me rend compte qu'il est un peut petit.
les deux ligne bleus sont
l+h
l-h
tu te souvient de h tu la vue dans les dérivées c'est une valeur qui tend vers 0.
ta définnission te dit que si ta suite converge vers L, il y a un rang k ou tout les u(k+n) sont compris entre l+h, et l-h.
le rang dépend de h.

par exemple
u(n) = 3sin(n) / n

cette suite converge vers 0
essaye de regader par exemple h = 1
sa veut dire que tout les termes de la suite, de rang supérieur a un rang k, doivent être compris entre 1 et -1.
essaye avec des h plus petit si tu sais utilisé ta calculatrice pour.
sinon fait toit rapidement un shéma sur une feuille

Supernick
rien a voir avec la définition de la suite, mais alors rien du tout.

remarque
normal
u(n) = f(n)

il suffit alors de dire. J'étudie la fonction représentative de la suite u(n).
et je me retrouve dans l'étude d'une suite, simple a faire, attention quand même, on n'étudie jamais la limite en une constante comme en 0, pour une fonction inverse, car sa ne sert a rien la suite étant définie par les entier elle ne peut pas tendre ( la variable x) vers une valeurs. donc la seule étude est en + l'infinie, c'est encore plus simple ( dans ce cas ) que d'étudier une fonction.

Merci Wayaht, je viens d'avoir un déclic grâce à toi !

Par contre, il y a une formule que je n'ai pas compris...
Il s'agit de cela :
Un réel a stricitement positif est donné.
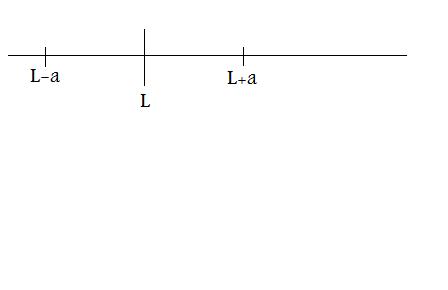
Pour prouver que la suite est convergente, il suffit alors de prouver que tout intervalle de la forme ]L-a ; L+a[ contient tous les termes Un de la suite à partir d'un certain rang p..
Ce qui se traduit par |Un - L| < a
Et là.. J'ai pas du tout compris. ^^ Je sais pas pourquoi ce chapitre me pose pas mal de soucis...
Merci encore !

le "a" ici est comme le h des dérivée, et celui que j'ai donnée dans mais exemples.

]L-a ; L+a[

on n'est d'accord que c'est la définissions de la convergence, donné précédemment. si tu imagine cela sur une ligne droite tu voit que ca signifie que la distance a L doit être plus petite que a. Or tu a vue en seconde que la distance s'écrit comme la différence des deux.

Un - L < a

or on ne sais pas si c'est Un ou L le plus grand donc on prend la valeur absolue comme sa pas de problème.

il y a d'autre démonstration si tu ne comprend pas celle la, je pense que c'est la plus claire mais ...

je refait le dessin je me suis tromper en l'enregistrant

voila

je me suis ramené a cet axe car seule les image m'intéresse pas les antécédents. imagine que sur cette droite il y a les différente valeurs de Un.

J'ai tout compris. Merci pour tout Wayaht !