Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première Translations - homothéties-rotationsTopics traitant de translations - homothéties-rotations [tout]Lister tous les topics de mathématiques
Niveau première
Partager :

Composée de rotations

Posté par
Othnielnzue23 31-05-20 à 15:55

Bonjour, j'ai besoin d'aide.

Merci d'avance.

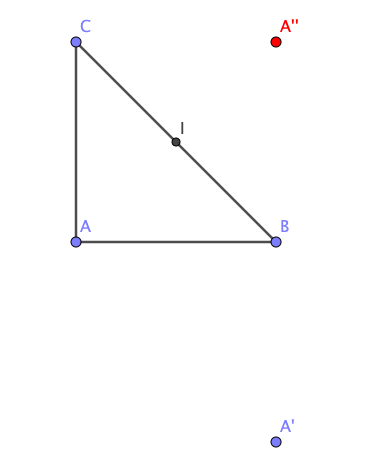
ABC est un triangle direct , rectangle en A et isocèle.

I est le milieu de [BC].

On pose f=r_{(A,\frac{\pi}{2})} o r_{(B,\frac{\pi}{2})}

1) Déterminer f(B).

2) Déterminer la nature et les éléments caractéristiques de f.

Posté par
malou Webmasterre : Composée de rotations 31-05-20 à 15:58

re
j'attends une rédaction (rédigée avec des phrases....que de pléonasmes ! ) correcte du 1er coup du type que je t'ai donnée dans ton précédent sujet

Posté par
Othnielnzue23re : Composée de rotations 01-06-20 à 09:27

Bonjour, voilà

1) r_{(A;\frac{\pi}{2})} et r_{(B;\frac{\pi}{2})}  sont deux rotations de centre A et B et d'angles \dfrac{\pi}{2}.

f(B)=r_{(A,\frac{\pi}{2})} o r_{(B,\frac{\pi}{2})}(B)


Or r_{(B,\frac{\pi}{2})}(B)=B car le centre est invariant

Donc r_{(A;\frac{\pi}{2})}[r_{(B;\frac{\pi}{2})](B)=r_{(A;\frac{\pi}{2})(B)


r_{(A;\frac{\pi}{2})(B)=C

car AB=AC et Mes(\vec{AB};\vec{AC})=\dfrac{\pi}{2}

Donc f(B)=r_{(A,\frac{\pi}{2})} o r_{(B,\frac{\pi}{2})}(B)
=C[/tex]

==>f(B)=C

Posté par
malou Webmasterre : Composée de rotations 01-06-20 à 09:38

à part le fait de réécrire la première phrase (qui est inutile, c'est l'énoncé), et n'apporte rien à cet endroit
ta question 1 est juste.
j'attends une question 2 nickel, du genre de ce que je t'ai rédigé hier.
prends le temps qu'il faut pour la rédiger, et relis toi pour être sûr que ton raisonnement est court et juste.

Posté par
mathafou Moderateurre : Composée de rotations 01-06-20 à 19:37

Bonjour

petit détail typographique pour être bien lisible
"o r" une fois passé dans la moulinette LaTeX est indiscernable de la conjonction française grammaticale (du texte) or (il supprime les espaces entre les lettres)

pour la composition des applications il y a un caractère fait pour
qui est \circ (pas la lettre o mais un rond) :

f(B)=r_{(A,\frac{\pi}{2})} \circ r_{(B,\frac{\pi}{2})}(B)

Posté par
Othnielnzue23re : Composée de rotations 02-06-20 à 09:02

Bonjour ,

2) f est la composée de deux rotations.


La somme de leurs angles est \pi donc f est une symétrie centrale ou une translation.

Or  f(B)=C donc le centre de f est le milieu de [BC].

f est la symétrie centrale de centre I.

Posté par
mathafou Moderateurre : Composée de rotations 02-06-20 à 09:47

La somme de leurs angles est pi donc f est une symétrie centrale ou une translation.

faux

donc ensuite raisonnement faux :
ce n'est pas parce que f(B) = C que l'on pourrait éliminer le cas "translation" (qui serait de vecteur \vec{BC} )

Posté par
PLSVUre : Composée de rotations 02-06-20 à 10:27

Bonjour
Déterminer    l'image de A    permet de justifier la réponse


Composée de rotations

Posté par
mathafou Moderateurre : Composée de rotations 02-06-20 à 11:15

une fois qu'on sait que c'est une rotation d'angle π, l'angle suffit
vu qu'il n'y a pas des tas de points Ω du plan avec   (\vec{\Omega B}; \vec{\Omega C}) = \pi   et  \Omega B = \Omega C

Posté par
Othnielnzue23re : Composée de rotations 02-06-20 à 11:27

Citation :
Bonjour
Déterminer    l'image de A    permet de justifier la réponse


Donc

t_{CB}(A)=A' et S_{B}(A')=A''

Posté par
mathafou Moderateurre : Composée de rotations 02-06-20 à 11:45

tCB ??? SB ????

de toute façon pour deux transformations quelconques f et g
on peut toujours écrire

f(n'importe quel nom de point) = ce nom '
puis g(ce nom ' ) = ce nom ''

sans que cela n'apporte quoi que ce soit à quelque raisonnement que ce soit ...
si on n'explicite pas ce raisonnement !

malou @ 31-05-2020 à 15:58

re
j'attends une rédaction (rédigée avec des phrases....que de pléonasmes ! ) correcte du 1er coup du type que je t'ai donnée dans ton précédent sujet

Posté par
Othnielnzue23re : Composée de rotations 02-06-20 à 15:27

f est la composée de deux rotations de centres différents .

La somme des angles des deux rotations est \pi=2k\pi (avec k\in \Z).

Donc f est la translation du vecteur \vec{BC}

Posté par
mathafou Moderateurre : Composée de rotations 02-06-20 à 15:42

pi n'est certainement pas pas égal à 2kpi
ou peut être voulais tu dire autre chose ?? se relire n'est pas en option ....
(AVANT de cliquer sur poster)

de toute façon ce que tu dis est faux. même en corrigeant la faute de frappe éventuelle
Revoir le cours vraiment et pas en citer des propos déformés !

de toute façon même sans cette règle (une fois qu'elle aurait été citée CORRECTEMENT et pas du n'importe quoi) :
il est évident en considérant l'image de A obtenue en composant les ROTATIONS de l'énoncé que A'' n'est pas l'image de A par une translation de vecteur BC !!

Composée de rotations

cette simple figure faite honnêtement
suffirait à éviter d'écrire des inepties ...

Posté par
Othnielnzue23re : Composée de rotations 03-06-20 à 09:56

Bonjour ,

f est la composée de deux rotations de centres différents .

La somme des angles des deux rotations est \pi.

\pi\neq2k\pi avec (k\in\Z) , f est une rotation.

Je ne sais pas comment faire pour trouver le centre de f

Posté par
Othnielnzue23re : Composée de rotations 03-06-20 à 10:03

Je sais que l'angle est \pi

Posté par
mathafou Moderateurre : Composée de rotations 03-06-20 à 10:06

mathafou @ 02-06-2020 à 11:15

une fois qu'on sait que c'est une rotation d'angle π, l'angle suffit
vu qu'il n'y a pas des tas de points Ω du plan avec   (\vec{\Omega B}; \vec{\Omega C}) = \pi   et  \Omega B = \Omega C


comment se traduit bien plus simplement que par une valeur d'angle le fait que   (\vec{\Omega B}; \vec{\Omega C})=\pi   ?

Posté par
Othnielnzue23re : Composée de rotations 03-06-20 à 10:34

Ben (\vec{IB}; \vec{IC})=\pi

Donc f est une rotation de centre I et d'angle \pi

Posté par
mathafou Moderateurre : Composée de rotations 03-06-20 à 10:54

ce n'est pas du tout l'étape de raisonnement que je demandais, mais la conclusion finale de tout. énoncée sans aucune justification.

tu n'as toujours pas compris ce que veut dire raisonner et rédiger.
ce n'est pas affirmer péremptoirement des conclusions tirées d'un chapeau !!!

de plus c'est incomplet.
n'importe quel point P du segment [BC] satisfait à   (\vec{PB}; \vec{PC})=\pi
et tu n'as pas justifié que même ailleurs il n'y en aurait pas

Posté par
Othnielnzue23re : Composée de rotations 03-06-20 à 11:05

Citation :
Ben (\vec{IB}; \vec{IC})=\pi et IB=IC

Donc f est une rotation de centre I et d'angle \pi

Posté par
mathafou Moderateurre : Composée de rotations 03-06-20 à 12:00

oui
en remplaçant le raisonnement de recherche du centre par une divination (que c'est peut être I) suivie d'une justification (que I convient effectivement car il satisfait aux conditions, qui est la seule et unique chose que tu as suggérée écrite)

j'attendais en suivant la chaine de raisonnement déja commencée sur la recherche du centre inconnu Ω
(on ne peut pas l'appeler I vu qu'il est inconnu !!)

(\vec{\Omega B}; \vec{\Omega C})=\pi
traduit le fait que ces vecteurs sont colinéaires et de sens opposé

c'était ça que je voulais te faire avouer
et par conséquent Ω appartient au segment [BC]

de plus &Omega:B = ΩC implique que Ω est le milieu I du segment

nota : une rotation d'angle π est une symétrie centrale
juste est donc aussi de conclure que f est la symétrie de centre I

pour la culture :
la composition de deux rotations, (de façon générale de deux isométries) peut se déterminer en décomposant ces deux rotations comme produits de symétries axiales que l'on choisit judicieusement comme partageant un axe commun aux deux rotations

Composée de rotations

il suffit alors de développer et de simplifier, puis retraduire en isométrie

Posté par
Othnielnzue23re : Composée de rotations 03-06-20 à 14:02

Pour les isométries je verrai plus tard.


Citation :
nota : une rotation d'angle π est une symétrie centrale
juste est donc aussi de conclure que f est la symétrie de centre I


C'est ce que j'avais vu dès le début , mais je n'ai pas su le dire ici.


Merci beaucoup,

Posté par
malou Webmasterre : Composée de rotations 03-06-20 à 14:09

et c'est la phrase qu'on attend dès le début.
Cet exercice tenait en 2 lignes en réalité.

Posté par
mathafou Moderateurre : Composée de rotations 03-06-20 à 14:38

"isométrie" = n'importe quoi parmi symétries, rotations, translations
ici il s'agit de rotations

malou : 2 lignes, tu exagères ..
selon le niveau de "preuve" exigé

les conclusions tiennent en 2 lignes, oui (une pour chaque question)
mais le pourquoi du comment , un petit peu plus tout de même !

malou @ 01-06-2020 à 09:38

j'attends une question 2 nickel, du genre de ce que je t'ai rédigé hier.
prends le temps qu'il faut pour la rédiger, et relis toi pour être sûr que ton raisonnement est court et juste.


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !