Inscription / Connexion Nouveau Sujet
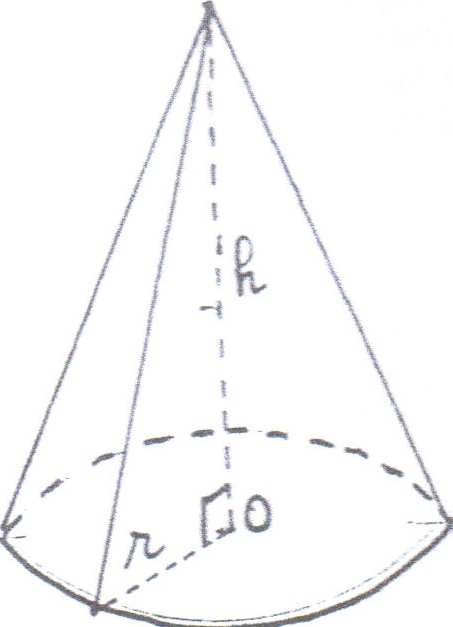
Cône de révolution
Bonjour,
Je vais essayer d'envoyer ma figure géométrique.
Soit M un point quelconque situé sur le cercle de centre O
La distance est constante. En connaissant r et h, on peut calcuer SM.
Quelle propriété faut-il utiliser ?
Je demande de l'aide car je ne vois pas du tout.
Merci .
Merci fanfan07
Connaissant SM et h, on peut calculer une mesure approchée de l'angle.... en utilisant le ...... d'un angle aigu. De même connaissant SM et...., on peut peut calculer une mesure approchée de l'angle.......
Je dois remplir ce texte à trou, et je ne vois pas ce qu'il faut mettre.
Connaissant SM et h, on peut calculer une mesure approchée de l'angle MSO en utilisant le cosinus d'un angle aigu. De même connaissant SM etr, on peut calculer une mesure approchée de l'angle SMO
je donne cette reponse mais il y en a plusieurs de valables !
regarde ton cours s'il n'y a pas deja eu une phrase semblable!
y aurait-il quelqu'un qui peut me répondre si :
[SO] est bien appelé la hauteur du cône.
et
(OM) est perpendiculaire à la hauteur [SO].
Merci de votre réponse.
Annuler
connectez vous