Inscription / Connexion Nouveau Sujet
cône de révolution
Bonsoir, je n'arrive pas a faire cet exercice:
Une entreprise de fonderie décide d'offrir à ces clients, comme cadeau de fin d'année, un presse-papier en forme de cône de révolution. Elle a à sa disposition des boules de terre réfractaire de 6cm de rayon. Le rôle d'un presse-papier étant d'être le plus lourd possible et la matière fondue étant homogène, la plus grande masse correspondra donc au plus grand volume. Le problème est donc de façonner ces boules des cônes de volume le plus grand possible. On rappelle que le volume d'un cône de révolution est V=
/3 R²x, où x représente la hauteur du cône et R le rayon de la base de ce cône.
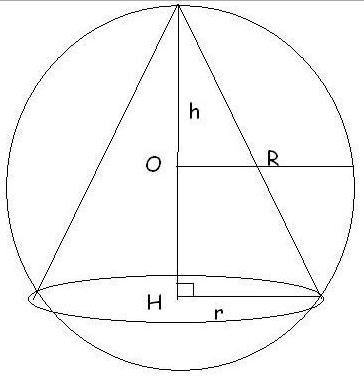
Partie A: Voici, ci-dessus, une perspective du cône de révolution inscrit dans la boule; la base du cône est le disque de diamètre [BC] et la hauteur du cône [AH]. On pose AH=x en cm. On remarquera que le point O appartient à la droite (AH).
1) Justifier le fait que 0 
x12
2) Représenter la section du cône par le plan ABC et calculer HC à l'aide de x. On commencera par calculer OH (soit lorsque x plus grand que 6, soit lorsque x6) puis OH².
3) Calculer en cm^3 le volume V du cône en fonction de x.
Partie B: Soit f la fonction définie sur [0,12] par f(x)=12x²-x^3. Soit C la courbe représentative de f dans un repère orthogonale (o;i;j) (unité graphique: 1cm en abscisse et 0.5 mm en ordonnée.)
1) étudier les variations de f
2) Résoudre sur [0,12] l'équation f(x)=0
3) Déterminer une équation de la tangente T1 au point d'abscisse 6.
4) Construire la courbe C (représenter en particulier la tangente T1)
Partie C:
1) Montrer que le volume du cône, en cm^3, est V=/3 f(x).
2) Interpréter dans le cadre du problème les solutions de l'équation f(x)=0.
3) Déterminer la valeur de x pour laquelle le volume du cône est maximum.
bonjour,
ce serait bien d'avoir
Voici, ci-dessus, une perspective du cône de révolution inscrit dans la boule;
je suppose que H appartient à [BC] et que A est le sommet du cône :
si BC=0, HA=x=2R=12 cm
si B, C et H sont confondus AH=x=0 cm
soit D le point diamétralement opposé à A
OD=R
HD=12-AH=12-x
OH=OD-HD=R-(12-x)=6-12+x=x-6
utilise Pythagore dans AHC pour calculer HC² puis le volume V
Bonsoir, je n'arrive pas a faire cet exercice:
Une entreprise de fonderie décide d'offrir à ces clients, comme cadeau de fin d'année, un presse-papier en forme de cône de révolution. Elle a à sa disposition des boules de terre réfractaire de 6cm de rayon. Le rôle d'un presse-papier étant d'être le plus lourd possible et la matière fondue étant homogène, la plus grande masse correspondra donc au plus grand volume. Le problème est donc de façonner ces boules des cônes de volume le plus grand possible. On rappelle que le volume d'un cône de révolution est V=/3 R²x, où x représente la hauteur du cône et R le rayon de la base de ce cône.
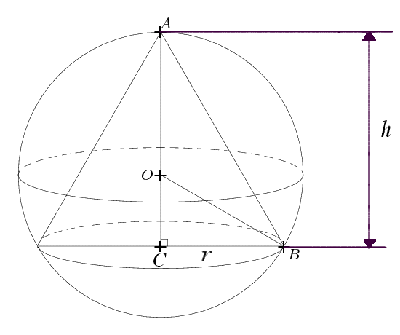
Partie A: Voici, ci-dessus, une perspective du cône de révolution inscrit dans la boule; la base du cône est le disque de diamètre [BC] et la hauteur du cône [AH]. On pose AH=x en cm. On remarquera que le point O appartient à la droite (AH).
1) Justifier le fait que 0 x12
2) Représenter la section du cône par le plan ABC et calculer HC à l'aide de x. On commencera par calculer OH (soit lorsque x plus grand que 6, soit lorsque x6) puis OH².
3) Calculer en cm^3 le volume V du cône en fonction de x.
Partie B: Soit f la fonction définie sur [0,12] par f(x)=12x²-x^3. Soit C la courbe représentative de f dans un repère orthogonale (o;i;j) (unité graphique: 1cm en abscisse et 0.5 mm en ordonnée.)
1) étudier les variations de f
2) Résoudre sur [0,12] l'équation f(x)=0
3) Déterminer une équation de la tangente T1 au point d'abscisse 6.
4) Construire la courbe C (représenter en particulier la tangente T1)
Partie C:
1) Montrer que le volume du cône, en cm^3, est V=/3 f(x).
2) Interpréter dans le cadre du problème les solutions de l'équation f(x)=0.
3) Déterminer la valeur de x pour laquelle le volume du cône est maximum.
*** message déplacé ***
Tu as eu des réponses, ici !
Reposter le même exercice cela s'appelle du multi-post est ce n'est pas toléré, ici !
en fait je voulais juste mettre une photo plus explicite
et la mauvaise foi en plus...l'image est déjà de l'autre côté
*** message déplacé ***
Annuler
connectez vous