Inscription / Connexion Nouveau Sujet
cône de révolution et sphère
Bonjour,
J'ai un DM de maths à rendre et je bloque à quelques endroits. Voici l'énoncé :
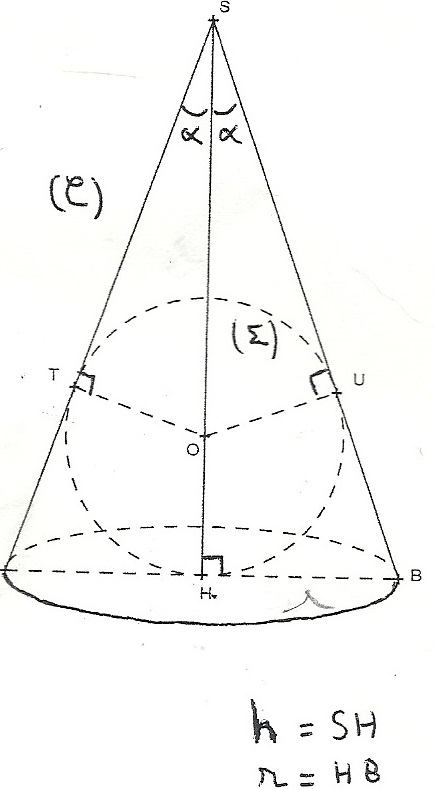
(£) est une sphère de centre O et rayon 6.
On souhaite l'on score dans une cône de révolution de hauteur h,d'angle au sommet S= 2a (alpha) avec une base qui est un disque de rayon r.
V le volume du cône doit être le plus petit possible
D'éternité h,r et a(la lettre alpha) ainsi que le volume minimal.
Où j'en suis :
J'ai essayé de chercher r en faisant Pythagore avec STO
J'ai trouver r au carré = 36h/h-12 mais je ne sais pas si c'est bon
Puis pour a (la lettre alpha) je pense qu'il faut faire la tangente de l'angle
Et pour h je pense Pythagore dans le triangle SHB mais il me faudrait la longueur r...
Voilà si vous avez des idées n'hésitez pas 
Merci d'avance !
bonjour
je vais chercher à exprimer r en fonction de h, pour établir la fonction volume, et rechercher le minimum de cette fonction
on remarque :
que h est supérieur à 12
que SO = h - 6
que le triangle HOU est isocèle en O, BHU isocèle en B, donc BU = BH = r, donc SB = SU + r
sur le tr. STO sin
= 6/SO = 6/(h-6)
sur le tr. SHB sin = r/SB = r/(SU+r)
produit en croix : 6(SU+r) = r(h-6)
SU² = SO² - r² = h(h-12)
donc SB² = 
h(h-12) + r
oups, validé par erreur, je souhaitais faire un aperçu de mes formules (la dernière ligne est donc fausse)
je reprends:
donc SB = h(h-12) + r
de ce qui précède : r = 6 [(h(h-12)) ] / (h-12)
V(h) = 1/3 * 
* r² * h = 12h²/(h-12)
étudie cette fonction sur ]12;+
[
tu dois arriver à un volume minimal pour h = 24
Bonjour,
merci beaucoup de votre aide marie84,je vais essayer de calculer le minimum de la fonction avec tout cela.
fm_31,hélas je n'arrive pas à accéder à votre lien :/
Annuler
connectez vous