Niveau première

Construction et utilisation chasles

Posté par
xiaxia 17-01-10 à 13:06

Bonjour, j'ai un exercice à faire et je bloque à la premiere question j'arrive à faire la premiere partie mais celle-ci ne correspond pas à la seconde.
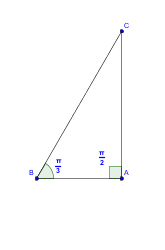
" On considere un triangle ABC avec(vect AB, AC)= -pi/2 et (vect BA, BC) = pi/3
1. Faire une figure
2. En utilisant la relation de chasles prouver que (vec CA,CB)= (vectAC, AB) + (vect BA, BC) + pi (2pi)
3. En deduire la mesure principale de l'angle orienté (CA,CB)"

Merci

Posté par re : Construction et utilisation chasles 18-01-10 à 11:50

Bonjour,

1) Construction et utilisation chasles

2) $(\vec{CA},\vec{CB})=(\vec{CA},\vec{AB})+(\vec{AB},\vec{CB})=(\vec{AC},\vec{AB})+\pi+(\vec{AB},\vec{CB})\;\;[2\pi]$

$(\vec{CA},\vec{CB})=(\vec{AC},\vec{AB})+(\vec{BA},\vec{BC})+\pi\;\;[2\pi]$

3) $(\vec{CA},\vec{CB})=+\frac{\pi}{2}+\frac{\pi}{3}+\pi\;\;[2\pi]$

$(\vec{CA},\vec{CB})=\frac{11\pi}{6}\;\;[2\pi]$

Et la mesure principale de $(\vec{CA},\vec{CB})$ est $\frac{11\pi}{6}-2\pi=-\frac{\pi}{6}$

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de maths

Fiches de niveau première
115 fiches de mathématiques en première disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

14 visiteurs

Changer d'île

Cours et Exercices de maths

Forum de maths

college

lycee

Outils de maths

Pages les plus populaires

Construction et utilisation chasles

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de maths