Inscription / Connexion Nouveau Sujet
côtés d'un triangle
 Timea
TimeaBonjour,
J'ai un souci pour résoudre ce problème.
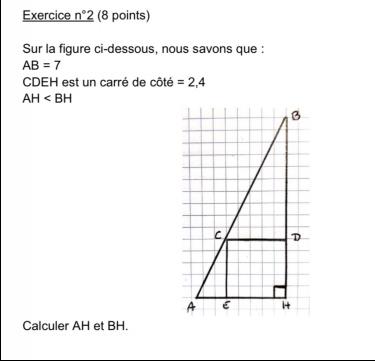
soit un triangle ABH rectangle en H tel que AB=7
On note C le point du segment [AB], D le point du segment [BH] tel que CDHE soit un triangle de côté 2.4.
On veut déterminer la longueur des côtés AH et BH.
J'ai tenté d'utiliser le théorème de Pythagore et le théorème de Thalès sans succès... Quelqu'un aurait-il une idée ?
Merci d'avance
Je pose x=AH et y=BH
j'obtiens y=Rac(49-x²) (y>0)
En appliquant Thalès dans les triangles AEC et AHB il vient :
AE/AH=AC/AB=EC/BH soit
(x-2.4)/x=AC/7=2.4/y d'où en remplaçant y par l'expression obtenue, cela donne : (x-2.4)/x=2.4/(Rac(49-x²))
puis en élevant chaque membre au carré, on obtient :
(x-2.4)²/x²=5.76/(49-x²)
Après développement j'obtiens l'équation :
x^4-4.8x^3-37.48x²+235.2x-282.24=0 équation qui me paraît difficilement résolvable en classe de première mais qui avec une calculatrice donne 4 valeurs de x qui sont x1=-6.772002 (à exclure car négative), x2=1.772002, x3=4.2 et x4=5.6
Est-il possible de trouver une solution plus simple et plus adaptée au programme de première ?
Une proposition, mais je ne sais pas si elle est plus simple à résoudre
En appelant x la longueur AE et y la longueur BD
on a d'où
on a aussi d'où
soit
on a d'autre part
on résout
Merci pour ton retour Hekla, j'ai pu ainsi obtenir les valeurs de AH=4.2 et BH=5.6 beaucoup plus facilement !
C'est ce que je trouve aussi. Il faut préciser que l'on n'a que cette solution parce qu'il a été posé AH<BH
De rien
Bonjour,
L'équation de degré 4 est juste mais sauf erreur de ma part, voici une autre solution niveau première rédigée un peu rapidement.
Soit x = AH et y = BH
Thalès : d'où xy = 2,4(x+y)
Pythagore : x² + y² = 49
On en déduit que (x+y)² = 49 + 4,8(x+y) donc (x+y)² - 4,8(x+y) - 49 = 0
D'où
On en déduit que xy = 23,52
On connaît la somme et le produit de deux nombres. Ils sont solution du trinôme : X² - 9,8X + 23,52 = 0
De plus, on sait que x < y.
On en déduit que et
Loin d'être évident toutefois.
Cordialement,
j4yF
Bonjour,
Je suis curieux de savoir comment vous avez résolu le système d'Hekla facilement.
Merci pour votre retour.
Bonjour,
Sylvieg vient de me conseiller cet exercice...
Tout d'abord dans l"énoncé un triangle de 4 sommets ????
Bon.
On voit que si AHB est aussi isocèle un tel carré mesurerait 2.475
ce qui signifie que les valeurs de AH et BH sont dans une fourchette
de 4 à 6
Je trouve personnellement avec la vérification AC+CB=7
que AH=4.2 et BH=5.6 (ou inversement)
Bonjour,
Je tente de répondre à la question de j4yF sur la résolution du système
2,42 = 5,76.
Pour la seconde équation, en développant et remplaçant 2,42 par xy, on obtient
(x+y)2 + (2 2,4)(x+y) - 49 = 0
2,4)(x+y) - 49 = 0
Ce qui permet d'obtenir x+y.
Bonsoir,
Je propose une résolution analytique de l'exercice.
On y penserait plus facilement avec un point A à droite du point H comme sur cette figure :
On choisit un repère d'origine H et de vecteurs et
.
On cherche a = HA et b = HB.
Les réels a et b sont strictement positifs.
La droite (AB) a pour équation .
Le point D est sur cette droite ; donc
Par ailleurs, on a
La première égalité donne .
D'où
On retrouve l'équation d'inconnue a+b :
La nuit porte conseil 
Inutile d'utiliser un repère. Il suffit d'ajouter les aires d'un carré et de deux triangles rectangles.
Toujours avec a = HA et b = HB :
L'aire du triangle AHB est ab/2
Celle du carré HA'DB' est 2,42
Celles des triangles AA'D et BB'D sont 2,4(a-2,4)/2 et 2,4(b-2,4)/2.
D'où 2,42 + 2,4(a-2,4)/2 + 2,4(b-2,4)/2 = ab/2
Ce qui donne 2,4(a+b) = ab.