Bonjour Grafen,

1. g ne s'exprimerait-elle pas plutôt, plus logiquement, par : 0,99x²+0,01x ?

2. Tu peux calculer correctement f(0,5) et g(0,5) ; ils sont évidemment <1 puisqu'il s'agit de proportions, et l'énoncé est faux quand il dit qu'il s'agit de pourcentages (une fois de plus : ras-le-bol des pourcentages, qui ne sont que des occasions d'erreur !)

3. A part ça, je ne suis pas sûr que la connaissance de la courbe de Lorenz d'une variable X permette de calculer sa médiane ... Confusion entre courbe de Lorenz et fonction de répartition ?

Bonjour , merci d'avoir répondu

J'ai recopier le sujet tel qu'il est écrit cependant g(x)=0.99x²+0.01x.
Concernant le nom du sujet il s'agit bien de courbes de lorenz . Je suis perdu . Est ce possible de faire f(0.5) x 9000 milliards pour trouver la médiane ?
Merci

Bien sûr que non : ça te donnera le patrimoine cumulé de la moitié des ménages qui en possède le moins (et même pas le patrimoine moyen de ces ménages, vu que tu n'en connais pas le nombre).

jai le meme exercice que toi a faire pourais tu m'aider stpppp ?

Bonjour Btisaam,

Que veux-tu que je te dise de plus que ce que j'ai déjà dit :
a) calcule f(0,5) et g(0,5) sans te tromper
b) la multiplication de f(0,5) ou g(0,5) par 9*10¹² donne le patrimoine cumulé de la moitié la plus pauvre de chaque pays, en aucun cas le "patrimoine médian" (médiane du patrimoine).
Trouver la médiane à partir de la connaissance de la courbe de Lorenz est un problème difficile, dont je ne suis pas sûr qu'il ait une solution. Il faudrait que les profs d'économie, qui ne sont pas tous des statisticiens, demandent conseil à ceux-ci avant que produire des énoncés qui n'ont pas de sens.

JE SERAIS D'AILLEURS CURIEUX DE VOIR LA CORRECTION DE CELUI-CI : peux-tu nous la communiquer ici dès que tu l'auras ?
Merci.

Voici un dessin essayant de montrer ce que je raconte :



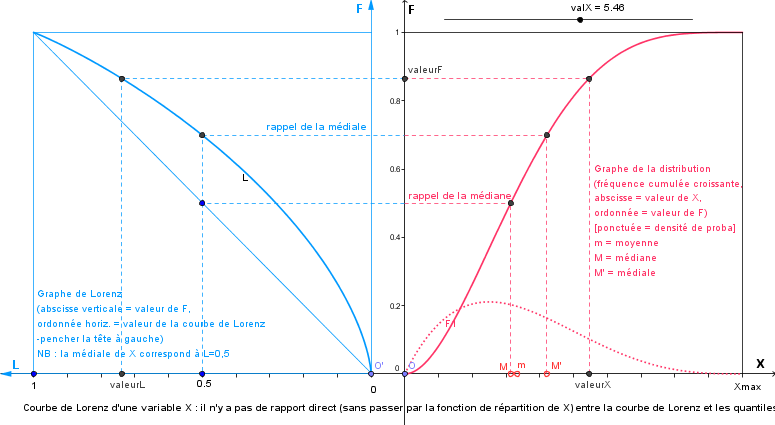
Il ne faut évidemment pas confondre quantiles ( valeurs de X [Xmin,Xmax] ) et quantièmes ( valeurs de F, proportions de la population [0,1] ).

Il ne faut pas non plus confondre, si X est par exemple le salaire individuel :
- médiane M = valeur de X qui sépare la population étudiée en deux selon le salaire individuel ; il y a autant d'individus en dessous qu'en dessus de M
- médiale M' = valeur de X qui sépare la population en deux selon la masse des salaires ; il y a autant de masse salariale en dessous qu'en dessus de M'.
La médiale M' est bien sûr supérieure à la médiane M dès qu'on s'écarte de l'égalité parfaite (salaire identique pour tous).

De rien ...

Pourquoi : 0,6 * 0,5[sup][/sup]+ 0,4 * 0,5 = 17 ??

"" 0,5 x²

Peux-tu poser ta question, en une seule fois (utilise le bouton "Aperçu" avant de poster), de façon correcte et circonstanciée ? Je pourrai alors peut-être y répondre ...

Pourquoi f(0,5) est égale à 17 ?
Désolé, je suis nouveau et ne connais pas encore très bien ce clavier :$
Pour g(0,5) je trouve le même résultat 25,25, mais pour f(0,5)je ne trouve pas le même.

Les deux sont faux. As-tu au moins lu mes messages avant de poser tes questions ?

Oui j'ai lue, mais pour g(0,5), le calcule donne bien 25,25, je ne voie pas en quoi cela est faux ?

Tu trouves vraiment que    0.99*0,5²+0,01*0,5 = 25,25  ?
A part ça, f(0,5) n'est en effet égal ni à 0,17 ni, encore moins, à 17.

G(x) est égale a 0,2525, donc oui après ça fait 25,25

Non : g(0,5) = 0,2525 , ce qui peut s'écrire 25,25% et sûrement pas 25,25.
D'autre part, évite de confondre minuscules et majuscules dans les symboles, avec une désinvolture qui rend la lecture fatigante. Merci.