Bonjour,

1) et 2) BON.

J'ai lu un peu vite ton coût marginal :

coût marginal=Cm(q)=C'(q)=3q²-24q+48

Tu as dû faire une faute de frappe!

4)

b)

Tu calcules CM(6)=6²-12*6+48

et C marginal : Cm(6)=3*6²-24*6+48

et tu vois que CM(6)=Cm(6)

J'ai sauté la 4) a) qui permet de répondre à la 4) b):

Merci beaucoup j'essaie de faire déjà ça et je vous redis ! Mais je n'arrive pas du tout à tracer les tangentes mais je vais déjà essayer jusqu'à la 4
Merci !

Pour la question 2 a il faut déterminer le tableau de variation de la fonction coût total j'ai donc fait :
q3 -12q2 + 48q
3q2 - 24q + 48
= b2 - 4ac
= 0 donc une solution donc j'ai fait = -b / 2a = 4 j'ai fait mon tableau mais je m'aperçois que pour la question 4 a il faut refaire la même chose, est-ce normal ?
Pour la 4b je ne comprends pas, pouvez-vous me détailler la réponse ?

Et pour les questions suivantes aussi.
Merci

Effectivement il y avait des erreurs dans l'énoncé j'ai donc changé. Il me faudrait l'exercice résolu pout comprendre , je dois regarder ca ce weekend pour mon devoir la semaine prochaine. Merci !
La coût total de fabrication de q centaines de picèes est donné par :
C(q) = q3 ( au cube) - 12q2 ( au carré) + 48q et C(q) est exprimé en milliers d'euros. On note C sa courbe représentative.
1. a Déterminer l'expression du côut marginal : 3q2 -24q+48
   b Déterminer l'expression du cout moyen : q2 -12q +48
2. a Déterminer le tableau de variation du coût total c'est fait :

q3 -12q2 + 48q
3q2 - 24q + 48
= b2 - 4ac
= 0 donc une solution donc j'ai fait  = -b / 2a = 4 j'ai fait mon tableau
3. Etudier les variations du coût moyen sur ]0;8] Comment faire ?

4. a  Effectivement il y a eu une erreur :  Résoudre 3(q-4)2 ( au cube) = q2( au cube) - 12q + 48
b Justifier que le coût moyen est minimal lorsque le coût moyen est égal au coût marginal
c  Déterminer l'équation de la tangente à C aux points dont l'abscisse esr solution de 4 a
d Que remarquer de la tangente à C lorsque le coût moyen est minimal ?
5- a Etudier les varaiations du coût marginal sur [o;8]; indiquer pour quelle quantité q0 le coût marginal change de sens de variation
b Déterminer l'équation de la tangent T à la courbe C au point d'abscisse q0
c  Déterminer les réels a, b et c tels que :
q3 - 12q2 + 48q - 64 = (q-a)(aq2 +bq + c )
d  Etudier le signe de q3 - 12q2 +48q -64 sur [0;8]
e Déduire de la question précédente la position de la courbe C par rapport à sa tangente F sur |o;8]
6)  a Résoudre C'(q) = 12
b  Déduire en quels points la tangente à la courbe C est parallèle à la tangente au point d'abscisse 6
7 Tracer les tangentes remarquables et celles étudiées puis la courbe C sur [o;8]

Déjà , ce qui n'est pas normal c'est que côut marginal et coût moyen n'aient pas de nom.

Je propose côut marginal =Cm(q).

et coût moyen=CM(q)

Et je refais ce que je t'ai envoyé et que tu n'as pas lu attentivement car tu me renvoies des calculs qu'il faut changer.

1)

a)

Cm(q)=C'(q)=3q²-24q+48

b)

CM(q)=C(q)/q=q²-12q+48

2)

C(q)=q³-12q²+48q

C'(q)=3q²-24q+48


C'(q)=3(q²-8q+16)

C'(q)=3(q-4)²

Donc C' est tjrs positif ou nul pour q=0 et C(q) tjrs croissant.

Il est inutile de calculer delta=0 comme tu as fait !!

3)Je te l'ai fait à 15 h 10 hier mais je recommence en utilisant la dérivée uniquement.

CM(q)=q²-12q+48

CM'(q)=2q-12

Cherchons quand CM'(q) > 0.

2q-12 > 0

2q > 12

q > 6

q--------->0..........................6....................8

CM'(q)---->............-...............0.........+..........

CM(q)----->48........décroît.........12.....croît........16

Car CM(0)=48 : CM(6)=12 ; CM(8)=16

On trouve ça en remplaçant q par ces valeurs dans CM(q)=q²-12q+46

4. a  Effectivement il y a eu une erreur :  Résoudre 3(q-4)² = q² - 12q + 48

Je devrais revenir demain dans l'après midi voir ça car ce weekend je ne suis pas là mais dimanche soir je reviendrai afin de comprendre cet exercice et de le finir entièrement !

Je vais t'en faire le max demain matin et je terminerai avant dimanche soir ... si je comprends l'énoncé !

Reconnais que l'énoncé est plus clair pour la 4) a) !!

4)
a)

Résoudre 3(q-4)² = q² - 12q + 48

On développe :

3(q²-8q+16)=q²-12q+48

3q²-24q+48=q²-12q+48

2q²-12q=0

2q(q-6)=0--->ligne (1)

Pour qu'un produit de facteurs soit nul , il faut que l'un  des facteurs au moins soit nul.

(1) donne :

q=0 ou q=6

En lisant ton énoncé je n'arrive pas à savoir si q[0;8] ou si q]0;8] ??

Disons donc que la solution de (1) est q=6.

Et on laisse q=0 qui voudrait dire que l'on ne fabrique rien.

4)

b)

Je pense que l'on veut une autre démonstration pour la 4) b)

4)

b)

Cm(q)=3q²-24q+48q

CM(q)=q²-12q+48

On va chercher quand Cm(q)=CM(q)

Il faut résoudre :

3q²-24q+48=q²-12q+48

Cette équa a été résolue en 4) a) et a pour solution q=6.

Et on a vu dans le tableau de la 3) que CM(q) est mini pour q=6.

Donc :

Le coût moyen est minimal lorsque le coût moyen est égal au coût marginal.

4)

c)

Déterminer l'équation de la tangente à C aux points dont l'abscisse est solution de 4 a

Donc équa de la tgte à C au point d'abscisse q=6

Le coeff directeur de la tgte est donné par C'(6) et C'(6)=Cm(6)=12

Donc équa tgte : y=12x+b

Il faut "b" . Elle passe par le point x=6 dont on calcule l'ordonnée que l'on trouve avec C(6):

C(6)=6³-12*6²+48*6=72

Donc la tgte passe par le point (6;72), ce qui permet d'écrire :

72=12*6+b qui donne b=0

Donc équa tgte à C au point d'abscisse : x=0 -->y=12x


4)

d)
Que remarquer de la tangente à C lorsque le coût moyen est minimal ?

Elle passe par l'origine .

5)

a)

Cm(q)=3q²-24q+48

Cm'(q)=6q-24

Cherchons le signe de Cm'(q).

6q-24 > 0

q > 24/6

q > 4

D'où le tableau de variation :

q-------->0.................4.................8

Cm'(q)--->........-..........0.........+........

Cm(q)---->48....décroît.....0.......croît.....48

Cm(q) change de sens de variation pour q₀=4

Note bien : on aurait pu raisonner tout autrement en remarqaunt que Cm(q)=3q²-24q+48 est représentée par une parabole orientée vers les q positifs car le coeff de q² est > 0 donc elle passe par un minimum pour q=-(-24)/(2*3)=24/6=4 et change de sens de variation pour q₀=4.

5)

b)

5)

c)

Déterminer les réels a, b et c tels que :
q³ - 12q² + 48q - 64 = (q-a)(aq² +bq + c )

Tu es sûre de ton énoncé?

Je suis sûr que c'est FAUX.

En fait , c'est :

Déterminer les réels a, b et c tels que :
q³ - 12q² + 48q - 64 = (q-a)(q² +bq + c )

J'ai perdu un temps fou à cause de cette FAUTE DE FRAPPE !! Fais attention !!

Il faut développer :

(q-a)(q² +bq + c ) qui donne :

q³+bq²+cq-aq²-abq-ac

soit :

b³+(b-a)q²+(c-ab)q-ac

Et on compare avec :

q³ - 12q² + 48q - 64

Par identification, on voit qu'il faut :

{b-a=-12
{c-ab=48
{ac=64

Et là, je n'ai pas réussi à résoudre ce système de 3 équas à 3 inconnues a, b et c. Désolé !!

Pour contourner l'obstacle, tu peux faire ce que j'ai fait.

Tu rentres dans ta calculatrice :

y=q³ - 12q² + 48q - 64

(la lettre q sera remplacée par x sur la calculatrice).

Tu affiches la courbe : elle coupe l'axe des x en x=4

donc a=4

car : ( q-a)(aq² +bq + c ) s'annule (vaut zéro) pour q=a qui donne :

( q-a)=0

qui explique  que ta courbe coupe l'axe des x au point x=4 (ou q=4)

Avec a=4 , on a facilement : b=-8 et c=16

Donc :

q³ - 12q² + 48q - 64 = (q-4)(q² -8q + 16 )

Tu peux vérifier en développant la partie droite. Tu retrouves la gauche.

5)

d)

5)

e)

Il faut corriger en 4) c) :
Donc équa tgte à C au point d'abscisse : q=6-->y=12x



6)  

a )

Résoudre C'(q) = 12

C'(q)=3q²-24q+48

3q²-24q+48=12

3q²-24q+36=0

3(q²-8q+12)=0

On doit résoudre : q²-8q+12=0

=(-8)²-4(1)(12)=16

=4

q₁=(8+4)/2=6

q₂=(8-4)/2=2

6)

b)

Déduire en quels points la tangente à la courbe C est parallèle à la tangente au point d'abscisse 6

Il faut C'(q)=12 car le coeff de la tge en q=6 est 12.

Donc l'autre  point cherché est  q=2

Je te souhaite bon courage avec un pareil exo et une abscence tout le WE.

Tu peux travailler jusqu'à plus de minuit dimanche !!

Pour tout arranger, moi aussi, j'ai fait une faute de frappe au 4) c).

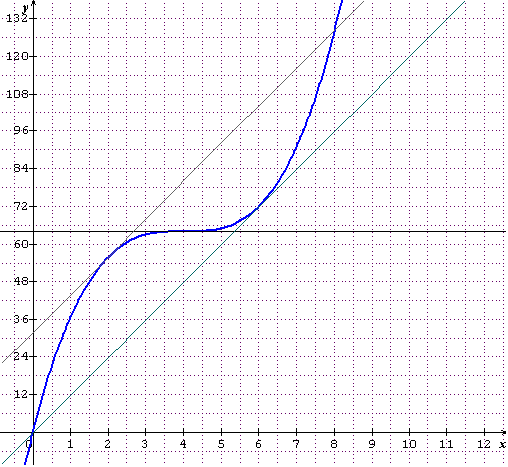
En bleu foncé : la courbe C.

En bleu-vert la tge T : y=12x

En gris-marron : la tgte // à T au point q=2

En noir : la tgte en q=4.

BON COURAGE !!