Inscription / Connexion Nouveau Sujet
cylindre inscrit dans une sphère
bonjours à tous,
je bloque sur un exercice d'application de la dérivation. J'ai (je pense) réussi les premières parties mais la question b me pose problème. Voila l'énoncé et un schéma de la figure :
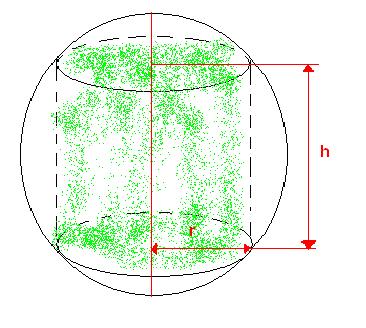
Dans une sphère de rayon R, on inscrit un cylindre de hauteur h. les deux bases du cylindre sont des cercles de la sphère de rayon r.
1) exprimer r en fonction de R et h
2) a) calculez le volume du cylindre en fonction de h
b) pour quelle valeur de h le volume est-il maximal?
merci d'avance
Bonjour
Quels sont tes résultats en 1 et 2.a ?
2.b) Dérive V(h) et cherche pour quelle valeur de h (en fonction de R) cette dérivée s'annule.
R²-h²/4
h (R²-h²/4)mais c'est après que viennent les problèmes je ne trouve pas les mêmes variations que sur le graphe de la fonction
Oui.
Et si la fonction V admet un extremum en a (ici, un maximum) alors sa dérivée s'annule en a : tu dois donc résoudre V '(h) = 0.
Annuler
connectez vous