Inscription / Connexion Nouveau Sujet
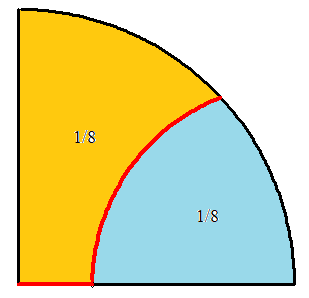
découpe d'un disque
Bonjour,
Inspiré par ![]() simplifier fct trigo reciproque
simplifier fct trigo reciproque
où il s'agissait de découper un disque en trois aires égales d'une certaine façon.
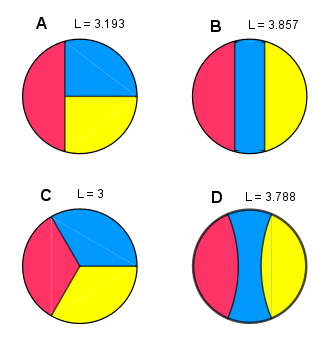
d'autres façons de découper en 3 aires égales (A est celle de l'exo) :
ou d'autres bien dissymétriques...
on peut s'intéresser à celle qui a une longueur de coupe totale minimale.
ici c'est l'évidente découpe C en 3 secteurs à 120°, L = 3 (pour un rayon de 1)
avec une découpe en 4 morceaux, le choix est plus large (figures de principe à main levée !)
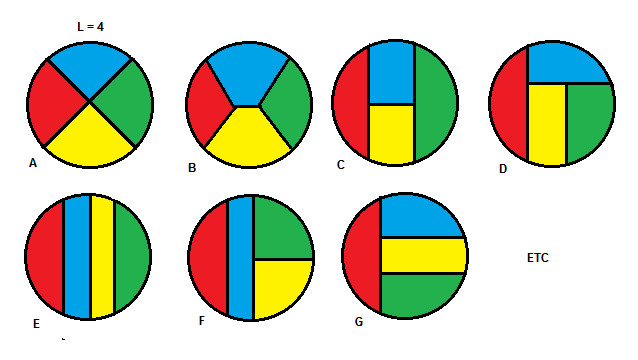
voire avec des découpes courbes !
on voit sur la découpe précédente en 3 bandes (B, D) que cela peut être avantageux (3.788 < 3.857)
le morceau rouge des découpes C,D,E,F,G est bien entendu identique et se calcule comme dans l'exo d'origine avec juste 1/4 au lieu de 1/3.
Quelle est celle avec la plus petite longueur de coupe ?
Bonjour
Sans réfléchir , je verrais bien le B avec des arrondis pour les morceaux verts et rouges . D'autre part , je me demande si la nature ne donnerait pas la réponse si on déposait quatre liquides non miscibles et en qualité et quantité identique dans un cylindre très plat 
Imod
la physique et les mathématiques se rejoignent dans cet exercice 
il faut calculer au moins avec des approximations pour éliminer les candidats de L > 4...
la B est effectivement la meilleure découpe en 4, y compris avec des segments de droite
Mais selon la longueur du segment horizontal, vu que à la limite on obtient A (segment nul) et ça (L > 6 !) :
(et au passage C)
donc beaucoup de valeurs > 4
reste à voir ce que l'on gagne ou pas avec des arcs courbes, mais là les calculs deviennent vite affreux.
Bonjour,
La piste des courbes ne convient pas en effet cette figure avec les 3 doubles secteurs circulaires gris foncés qui semble optimale (avec un angle de 101.20384°):aire unitaire 0.7854 =aire jaune ( /4.
/4.
La corde mesure 0.154551
soit les 3 :0.463653
Remords:
Je pensais que vous étiez sur L <4 pour la division en 4 ....
mais en vérifiant L de B je trouve 6.657 donc 5.3 est nettement
meilleur.
le minimum à chercher est bien < 4
avec ta découpe, l'optimum est :
(obtenu quand les cercles sont orthogonaux)
L= 5.25 > 4 donc cette découpe est à rejeter puisque A est meilleure..
pour B, ça dépend de la longueur du segment horizontal
on peut trouver une des longueurs de ce segment pour lesquelles L total < 4
Effectivement pour les figures avec arc de cercles on n'aura pas mieux <5.25
Pour la figure B en "diabolo" avec des segments ,j'ai optimisé pour obtenir 4 S de  /4,j'ai trouvé un segment central de
/4,j'ai trouvé un segment central de
0.694114882 avec 4 obliques de 0.91253914 donc on dépasse (4.344 )
ton segment central est bien trop grand pour avoir un minimum de L
il faut avoir la longueur 2a de ce segment < 0.415 pour avoir L < 4.
comme suggéré dans mon message
"Mais selon la longueur du segment horizontal, ..."
ça veut bien dire qu'il existe une infinité de ces longueurs compatibles avec l'égalité des aires
toutes ces figures dérivées de la configuration B ont les aires = pi/4 "par construction"
à la précision du calcul car pour chaque valeur de cette longueur = 2a, il faut résoudre une équations du genre x - a sin(x) = cte. ce qui ne peut se faire que par approximation numérique, c'était le thème de l'exo d'origine, pour obtenir l'angle au centre = la position de D garantissant aire = pi/4)
Bonjour,
Je ne comprenais pas pourquoi pour B j'avais faux....Au réveil j'ai vu mon erreur (certainement classique), je mettais 120° comme angle au centre
pour chercher le minimum de L il ne faut pas fixer l'angle à priori de toute façon.
Ma valeur de 120° de l'angle A est juste un exemple, ce n'est pas l'optimum
avec 120° pour l'angle au centre j'obtiens d'ailleurs L = 4.158
on peut faire un peu mieux que 3.96
et une fois que on a obtenu le minimum avec des segments de droite, on peut encore améliorer avec des courbes "judicieuses".
mais ça joue sur des fifrelins.
Si mes souvenirs sont bons , il ne faut chercher qu'avec des segments de droites et des arcs de cercles .
Imod
Je me souviens de certains bâtons qui ne devaient pas passer dans des grilles avec Imod et derny entre autres.
On peut garder cette recherche "idéale" pour l'hiver 
oui
en vertu de :
le plus court chemin entre deux points est une droite
et : la courbe de longueur minimale entourant une aire donnée est un cercle.
après on découpe ça en morceaux et on regarde ce qu'il se passe aux jonctions...
(je pense que ton résultat est toujours avec des segments de droite, tu ne le précises pas)
en tout cas on peut faire mieux, même avec des segments.
j'ai 3.95126...
bon, maintenant il va falloir atteindre 3.9457 avec des parties courbes ...
et déja étudier la "théorie"
on sait déja que chacun des 5 "segments" de cette découpe B est un arc de cercle ou un segment de droite
comment doit on les raccorder pour obtenir un minimum ?
on a certes 1/8 + 1/8 de l'aire du quart de disque 
mais il existe de très nombreux arcs de cercles pour faire cette découpe, et il s'agit de trouver celui qui donne la plus petite longueur rouge
(hum, pas vraiment : la plus petite valeur pour 4 arcs + 2 segments !! ça change beaucoup le résultat !)
indice : X13 de l'ETC a son mot à dire dans la "théorie", préalable incontournable, qui justifie ce qu'il se passerait avec ton expérience de physique...
Je ne vois pas trop de quoi tu parles avec ton indice 
En complétant mon dessin par symétries , on a juste un segment et deux demi-cercles mais apparemment on peut faire mieux .
Imod
l'arc de cercle le plus court découpant le quart de disque en deux est
on a bien une meilleur découpe que le rayon pour un quart de disque,
ou même que en le coupant par un cercle concentrique
mais hélas appliqué au problème global, il donne L = bien trop grand !
en prenant la figure complétée par symétrie, au "mieux" (pas facile car il y a deux variables à régler en faisant ainsi)
on obtient ça :
j'ai ici choisi les deux cercles de même rayon
avec un rayon différent on ne gagne pas grand chose, en tout cas je n'ai pas réussi à avoir L < 4 ainsi.
comme le X13 n'a pas tilté je mets un indice :
on a deux "théorèmes" le I et le II
en appliquant ces deux théorèmes au voisinage immédiat de N et de P, on en déduit comment se "raccordent" des bulles de savon ... (entre elles et avec une paroi)
Pour les segments,je pense qu'on est au minimum .L'équation est assez difficile ,mais on peut procéder par essais et 3.95 par exemple est impossible à obtenir.
J'ai essayé un arc de cercle de 28 ° et de Rayon 2 qui encadrerait le segment oblique en respectant les aires et on arrive à  4 .
4 .
Je pense que la piste des courbes va être dure....
Le premier résultat est connu , le point P est le point de Fermat qui correspond à des angles de 120° quand c'est possible et à un sommet du triangle dans le cas contraire . Le deuxième résultat ne me parle pas 
Imod
pour les segments j'ai opéré ainsi :
le paramètre libre est la longueur du segment horizontal
plus exactement la distance OA = a
je cherche alors l'angle au centre qui donne l'aire = pi/4
plus précisément l'angle t qui donne l'aire hachurée = pi/8
cette aire est l'aire du secteur circulaire OIB moins celle du triangle OAB
c'est à dire avec t en radians :
la fraction de l'aire du disque
moins
Aire =
on obtient donc finalement l'équation
cette équation ne peut se résoudre que par approximation (par exemple avec la méthode de Newton)
on reporte alors cette valeur de t pour calculer AB (al Kashi) et donc la longueur L de la découpe .
on peut faire tout ça avec Geogébra
intersection de la courbe de avec l'axe des abscisses
puis rotation de centre O du point I, de l'angle = l'abscisse du point d'intersection
(c'est Geogebra qui se charge de Newton)
on ajuste alors A à la main pour rendre L minimale.
ou bien écrire un petit programme en Python ou autre pour faire ça
et même alors automatiser la recherche du a rendant L minimum par dichotomie.
(pas fait)
pour les arcs de cercle (arc au lieu de segment AB) j'ai opéré autrement car il y a à priori deux paramètres libres au moins.
"la Théorie" permet de n'en garder qu'un seul : a
mais alors je construis B et l'arc selon "la théorie" et j'ajuste A pour avoir l'aire = pi/4
@ Imod
oui point de Fermat = X13 selon la nomenclature de l'encyclopédie des points remarquables d'un triangle (ETC Enyclopedia of Triangle Centers ![]() )
)
sous Geogebra la commande TriangleCentre(A,B,C,13) le donne directement
Le deuxième résultat ne me parle pas
quand il y a plusieurs normales possibles issues de M, on ne garde que la plus courte.
>mathafou,
Pour mon test ,j'ai pratiquement fait comme toi.
je teste a qui avec la règle des cos me donne l'oblique puis la demi corde.
Une fois obtenu une aire de  /4 pour la figure Est
/4 pour la figure Est
Je vérifie que j'obtiens aussi  /4 pour la figure Nord.
/4 pour la figure Nord.
A l'envers ,je teste les valeurs inférieures pour L ,je ne vois rien de < que 3.951....
1/2 ( 1 - 2 x 1/4) est fatalement = 1/4
à l'envers (connaissant L en déduire l'angle) me semble plus compliqué
je confirme que avec des segments de droite on ne peut pas obtenir moins que
j'ai 3.95126...
il faut courber les segments inclinés AD etc pour faire (un tout petit peu) mieux :
mais là les calculs proprement dits deviennent affreux et j'ai renoncé à en faire.
ce sont des résultats affichés par Géogébra
A a été ajusté "à la main" pour que l'aire soit bonne à 10-10 près,
le reste est de la construction géométrique exacte à partir de ce point A.
je rappelle que le segment horizontal mesure 2a dans cette figure.
(voir celle de 10h39 pour les segments de droite, avec des arcs c'est pareil)
C'est la configuration que j'avais en tête avec mon dessin 08/05/24/18:34 et il n'y avait en effet aucune raison que les arcs supérieurs et inférieurs se raccordent tangentiellement .
Je ne pense pas qu'on puisse faire un calcul explicite du périmètre minimum mais j'y reviendrai quand je serai moins occupé par ailleurs . Joli problème 
Imod
Effectivement un joli problème.
>mathafou ,
Pourrais-tu me donner le Rayon de la courbure car moi dans mon essai j'avais pris 2 sans succès ? Le tien doit être plus grand .Merci.
il était écrit dans ma figure du 09-05-24 à 15:54 :
R = 4.661...
mais sans "laThéorie", il y a trop de paramètres libres à faire varier
Imod : Je ne pense pas qu'on puisse faire un calcul explicite
on obtient des équations qui sont un mélange de polynômes (voire même pire avec des racines) et de fonctions trigo (exponentielles logarithmes etc)
ici on obtient, même déja avec des segments, une équation de la forme
qui ne peut pas se résoudre autrement que par approximations successives
(la chèvre c'est avec un truc en "polynome +arctan = cte", c'est pareil)
ce sera même bien pire avec des arcs de cercle.
reste que avant même d'écrire quelque calcul que ce soit, la règle "des films de savon" s'applique
en reprenant mes figures de 08-05-24 à 20:37
en raisonnant au voisinage de N par le théorème II :
toute courbe de longueur minimum libre par ailleurs rencontrant une paroi fixe (c) la coupe à angle droit.
en raisonnant au voisinage de P par le théorème I (Fermat / Torricelli) :
à tout point triple d'une courbe de longueur minimale, les tangentes sont à 120°
on applique ça ici en modifiant la recherche d'une courbe minimale entourant une aire donnée en la recherche parmi toutes les courbes minimale de celle qui entoure une aire donnée.
conséquence dans la figure de la découpe en 4 avec des arcs de cercles :
| les arcs de cercles ont leur tangentes en A à 120° et sont orthogonaux au cercle du pourtour. |
une construction géométrique à partir du point A :
une droite en A à 30° coupe le cercle en U et V
soit T le conjugué harmonique de A par rapport à (U, V)
et W le milieu de AT
le cercle cherché est le cercle de diamètre AT (de centre W)
il ne reste plus qu'à faire varier A pour avoir la bonne aire.
>mathafou

J'en ai profité pour voir ton site sur les harmoniques.
Ici UV est assez dur à calculer avant d'avoir le rapport....
Donc,je pense que le L minimum est atteint .
Pour le calcul on peut commencer ainsi :
OM = a sin(30°) = a/2
MV² =OV² - OM² = 1 - a²/4
MA.MT = MV² (division harmonique), donne MT
puis R = (MT-MA)/2
on a ainsi le rayon en fonction de a
ensuite OW² = 1 + R²
on peut faire alors les calculs des angles et donc de l'aire et des longueurs des arcs :
(OF, OW) = arc cos(a/(2OW))
(OW OD) = arc cos(1/(OW))
et (OF, OI) = 30°
en combinant, cela donne l'angle (OI OD) donc l'aire du segment de disque ID
etc
c'est assez pénible tout ça mais ça devrait aboutir au final à l'aire et la longueur en fonction de a
or on veut cette aire là = pi/8 ... donc on résout en l'inconnue a
et on obtient la longueur qui est "par construction" (= "la Théorie") le minimum.
déja dit que la résolution d'une telle équation ne peut se faire que par approximations successives. (absolument incontournable quelle que soit la méthode de calcul employée)
pas dit que choisir une autre variable que a soit plus simple.
Je me suis lancé un peu follement dans la construction de bulles 
![]()
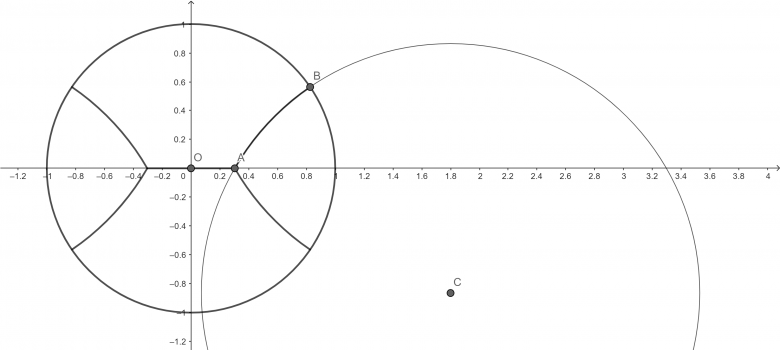
J'obtiens bien la même réponse que mathafou.
Je suis parti dans les nombres complexes et ça se simplifie pas mal 
Soit l'angle AOB,
l'angle ACB et
le rayon du grand cercle.
On a:
La partie imaginaire de est nulle. Donc
.
La distance OA est donnée par
Et la longueur de l'arc de cercle ACB est donnée par .
Et on a une longueur totale donnée par
L'aire à droite quand à elle est donnée par
En résolvant on obtient
Ce qui donne:
joli calcul !
finalement passer aux affixes est bien la plus efficace façon de le faire.

(en les refaisant, bon exercice, on détecte quelques fautes de frappe / recopie)
Pour 5 bulles, c'est bien plus simple 
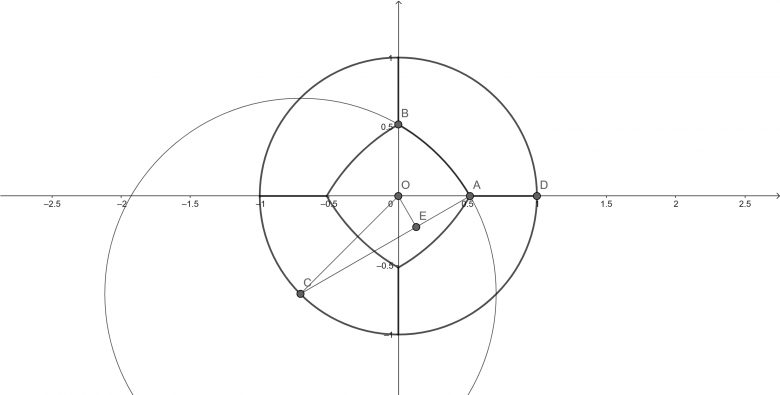
Soit la distance OC.
La distance AC est donnée par
L'aire du centre est donnée par .
En résolvant , on obtient
Donc C, n'est pas tout à fait sur le cercle.
L'arc ACB est donné par
La longueur totale est de
Je ne pense pas qu'il y ait mieux 
L'élément central fait penser à un carré dessiné sur une sphère 
Sans forcément faire tous les calculs , je serais curieux de voir la disposition des différents éléments avec forcément pleins de symétries dans le cas 6 , 7 , 8 ... bulles
Imod
Avec du calculatoire basé sur les conseils éclairés :
Le L champion est 3.9457............
Donc par rapport à l'intuition 4 un gain de1.35 %
Sur le plan pratique rien ne vaut la découpe selon les deux
diamètres perpendiculaires.
Je pense que la nature est bien plus exigeante que toi et ça devrait sans doute se voir quelque part 
Imod
Bonjour
pour 5 il y a une erreur sans doute de recopie :
a = 0.48317... OK (je trouve pareil)
arc b = 0.7393... OK aussi
4a+4b = 4.88997...
en fait avec 5 on peut mieux faire (4.835...) mais plus compliqué :
je doute qu'on s'en sorte avec des des calculs simples
j'ai fait par réglages des points libres A et B pour avoir S1 et S2 = pi/5
pour 6 j'ai :
les symétries permettent de n'avoir qu'un seul point de réglage.
et le même principe de calcul que pour 4 avec juste une valeur différente de l'aire.
le problème est que avec des n grands il y a une "explosion" combinatoire des arbres de Steiner(*) possibles ...
et donc à moins d'y passer sa vie, on ne peut pas garantir que la configuration choisie sur laquelle on a passé déja beaucoup de temps de calcul / ajustements est la meilleure.
(*) un problème plus simple est de relier n points par un réseau minimum = arbre de Steiner
par exemple la vidéo là ![]() youtube
youtube
ou plus "universitaire" le document ![]() (mémoire de licence)
(mémoire de licence)
cela pourrait faire l'objet d'une autre discussion, par exemple sur la construction (à la règle et au compas) de ces arbres.
au delà de n = 4 ou 5 cela devient affreux.