Inscription / Connexion Nouveau Sujet
définition d'une fonction
Bonjour,
On considère la fonction f définie par f(x) = et Cf sa courbe représentative.
1) donner l'ensemble de définition de la fonction f
2 étudier la position relative de la courbe Cf et de la droite D d'équation y = -x +3
1) la fonction est définie pour tout x différent de x = -1
x2 - x +1
si .
Comment faire sa courbe représentative ? Elle ne doit pas couper l'axe des abscisses.
Merci
Bonsoir kikipopo
OH !!!
On ne vous demande pas la représentation graphique
la courbe est en deux morceaux
bonjour,
1) attention, tu fais une erreur.
2) tu veux dessiner la courbe ?
tu peux le faire sur ta calculatrice ou sur geogebra..
mais pourquoi faire au juste ?
encore une erreur de signe , mais dans l'énoncé qui x +1
c'est donc bien x
pourquoi la courbe ? Pour donner la position relative de Cf et de l'axe des abscisses.
la question est
2) étudier la position relative de la courbe Cf et de la droite D d'équation y = -x +3
la position de la courbe avec l'axe des abscisses importe peu..
comment fais tu pour etudier la position relative de Cf et (D) ?
Donc si le dénominateur est x+1 alors oui la fonction n'est pas définie pour
On vous demande la position de la courbe par rapport à la droite d'équation
l'axe des abscisses ne nous intéresse absolument pas
Principe
On considère un point M appartenant à la courbe représentative de . Il a donc pour
coordonnées .
On considère maintenant un point N de même abscisse que M, appartenant à D j'appelle g la fonction dont est la représentation graphique
Le point N a donc pour coordonnées
Pour étudier la position relative des deux courbes, on veut savoir si l'ordonnée de M est plus grande que l'ordonnée de N ou le contraire.
est équivalent à
ou encore
On étudie donc le signe de la différence
si alors
par conséquent la courbe représentative de
est au-dessus de la courbe représentative de
si alors
par conséquent la courbe représentative de
est au dessous de la courbe représentative de
si alors on a un point d'intersection des deux courbes
Bonjour,
Merci beaucoup.
Je croyais que vous étiez parti,
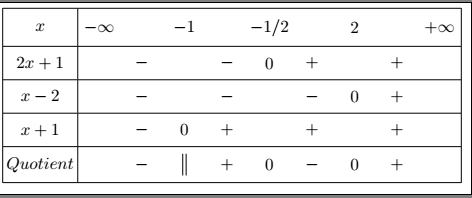
J'avais fait un tableau en tenant compte de la valeur interdite mais qui ne correspond pas pour moi au graphique donc je ne l'ai pas conservée .
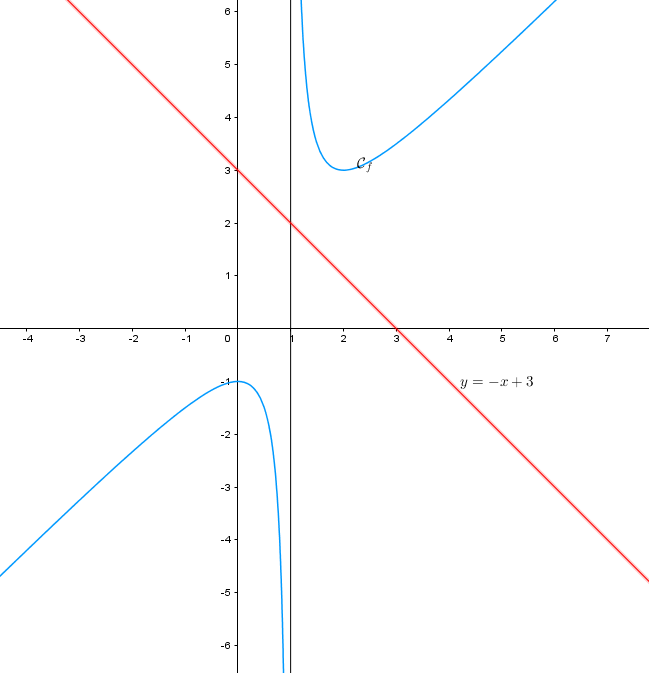
D'après le graphique , la parabole est au-dessus de la droite entre
Et d'après le tableau de signes, c'est le contraire.
Je ne sais pas comment l'expliquer.
Bonjour
Ce n'est pas une parabole, c'est une hyperbole, mais non rapportée à ses asymptotes.
La courbe représentative de est bien sous la droite lorsque
ou sur l'intervalle
La courbe représentative de est en bleu et la droite en rouge
C'est bien ce que l'on constate sur le graphique
Oui, je n'avais tenu compte que de la partie de l'asymptote au-dessus de l'axe des abscisses.
En revanche ce qui n'est pas clair pour moi, c'est la valeur interdite.
J'ai bien compris qu'elle rendait la résolution du trinôme impossible : un quotient par 0 est impossible. Mais on tient bien compte pour établir le graphique. et rédiger la solution.
On est bien obligé de tenir compte qu'en il y a un problème, une rupture, on passe de
à
.
Il est vrai que certaines calculatrices posent problème à cause de l'épaisseur des pixels. On a l'impression que la courbe est continue.
Seul le numérateur est un trinôme du second degré, la fonction forme un tout c'est une fraction qui n'existe que si le dénominateur est non nul
« Valeur interdite » fut sans doute un raccourci, pour dire que la fonction n'avait pas de sens lorsque le dénominateur était nul
C'est à dire que si
,
le quotient est impossible.
"On est bien obligé de tenir compte qu'en -1 il y a un problème, une rupture, on passe de -\infty à +\infty."
je ne vois pas de rupture sur le graphique ou je ne sais pas ce que vous appelez rupture.
Vous pouvez résoudre cette équation, le ici n'est pas un problème. Ce n'est pas
une valeur que l'on donne à , on cherche justement la valeur qu'il faudrait
donner pour que cette fraction vaille
Ces valeurs étant différentes de , elles sont bien solutions
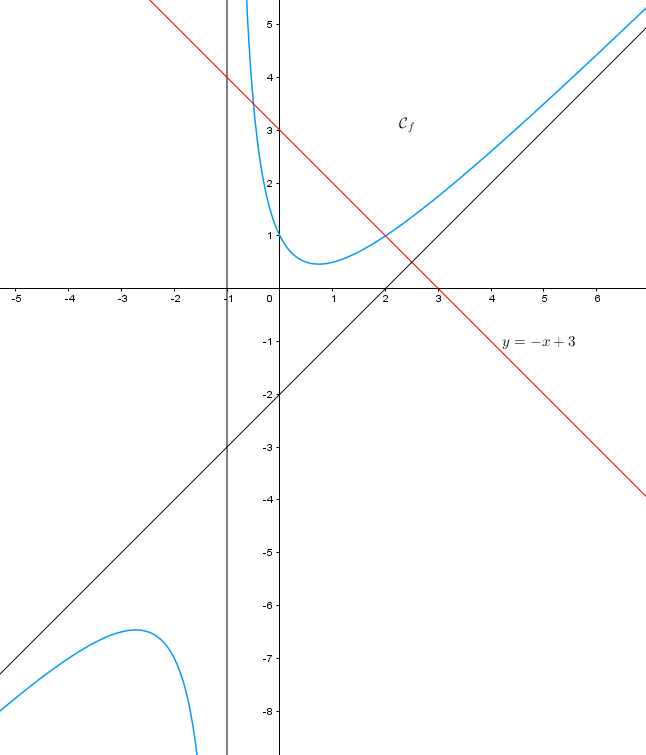
Sur le graphique a été tracée la droite d'équation
À gauche un morceau en bleu tente de se rapprocher de cette droite tandis qu'à droite le morceau semble s'en éloigner et rien ne permet de les recoller. C'est bien ce que j'appelle une rupture entre ce qui se passe à gauche et ce qui se passe à droite. Il y a bien une discontinuité. Vous ne pourrez pas construire la courbe sans lever à ce moment le crayon pour poursuivre le traçage de la courbe
D'accord pour la rupture : c'est dénominateur x+1 qui en est responsable.
"Vous pouvez résoudre cette équation, le -1 ici n'est pas un problème. Ce n'est pas une valeur que l'on donne à x, on cherche justement la valeur qu'il faudrait donner pour que cette fraction vaille -1"
Pourquoi dites-vous que -1 est la valeur du quotient qui est recherchée ?
On peut l'écrire autrement C'est bien chercher les antécédents de
c'est-à-dire résoudre l'équation
Qu'est-ce résoudre une équation si ce n'est trouver les valeurs pour lesquelles l'égalité est vérifiée
C'est-à-dire que si
le quotient est impossible.
Vous avez écrit cela à 14 h 47. Depuis j'essaie de montrer que le
Je vais relire tout ce que vous avez écrit et essayer de comprendre où je bute.
Je comprends juste le contraire de ce que vous écrivez :
"on cherche justement la valeur qu'il faudrait donner pour que cette fraction vaille -1"
Pour moi, on cherche les valeurs qu'il faudrait donner pour que la fraction vaille
Ce qui est le cas, dans votre démonstration.
Si vous écrivez
soit c'est une affirmation
soit c'est une équation et on cherche quand cette égalité est vraie
Si l'on écrit alors on va travailler sur l'ensemble des réels à l'exclusion d'icelui.
J'ai compris.
Je dois démontrer que cette affirmation est fausse en trouvant les
valeurs qui le prouvent.
Merci beaucoup.
Malheureusement, je risque d'avoir encore des choses difficiles à comprendre au cours des prochains jours.
Mais pour aujourd'hui, tout est clair.
Sûrement à demain ou après-demain.
Bonne soirée.
C'est bien
Vous avez raison de poser toutes les questions jusqu'à ce que ce soit clair. J'essaierai d'y répondre le plus précisément possible.
Bonne soirée