Inscription / Connexion Nouveau Sujet
Demi droite d'un rectangle et fonctions associées
Bonjour,
Soit ABCD un rectangle tel que AB=4 cm BC=6cm. Un droite variable extérieure au rectangle et passant par C coupe la demi droite [AB) en M et [AD) en N. On pose BM =x et AN= y
1. Etablir un relation entre y et x.
2.En déduire une expression de y en fonction de x, puis démontrer en utilisant les fonctions associées que y est décroissante de x sur [0;+¤]
Je n'arrive absolument pas à répondre à ces deux questions, j'ai vraiment besoin d'aide s'il vous plait. Le symbole ¤ veut dire "infini"
J'espère une rapide réponse, merci d'avance.
Bonsoir
As-tu pensé à faire un schéma ? En le faisant, on pense (normalement) tt de suite au tm de Thalès et ça permet de répondre oà la Q1.
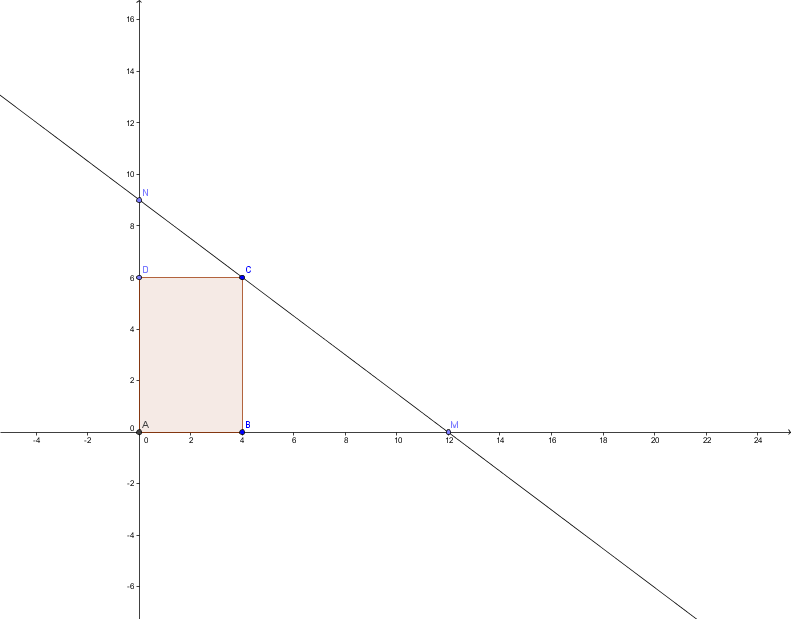
D'après le schéma, en application du tm de Thalès, on a
avec NA = y ; ND = y-6 ; DC = 4 ; AM = 4+x
Dc
Q2.
des égalités ci-dessus, on déduit : (y-6).(4+x) = 4y.
Après développement et simplifications, on a :
, soit
démontrer en utilisant les fonctions associées que y est décroissante
Avec un tel énoncé, je suppose qu'on ne te fait pas utiliser les fonctions dérivées (que tu n'as p.e. pas encore vues, cet exercice pouvant servir d'introduction par la suite aux fonction dérivées "simples")
Dc il faudrait utiliser les fonctions de références étudiées en secondes.
Une fonction du type
;0[ et ]0;+[ ( je crois que tu t'est trompée ds le sens de tes crochets)
dc, même si on rajoute +6 à
[ ,puisque :
d'accord ?
Annuler
connectez vous