Inscription / Connexion Nouveau Sujet
démonstration
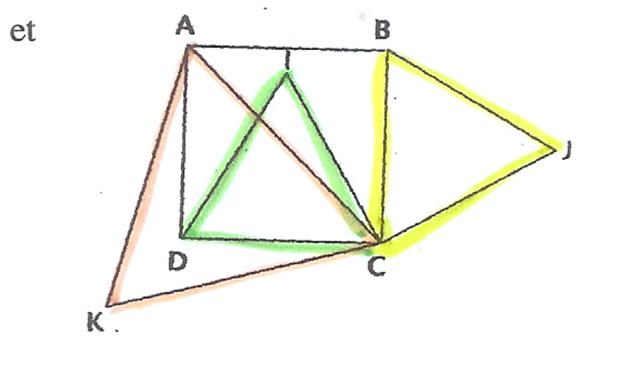
Bonsoir, je n'arrive pas à faire cet exercice et j'ai donc besoin de votre aide: ABCD est un carré et ACK, CDI, BCJ sont des triangles équilatéraux.
a) Démontrer que B, D, K sont alignés.
b) En déduire, à l'aide d'une rotation de centre C et
d'angle +pi/3, que A, I, J sont alignés.
a) pour la question je voudrais utiliser des angles orientés, dire que c'est égale à pi, et donc conclure qu'il sont alignés, seulement je ne vois pas comment faire...
Merci de votre aide 
Bonsoir,
Un petit coup de main pour la question a) histoire de te mettre le pied à l'étrier.
Le carré ABCD a ses diagonales qui se coupent en leur mileu et perpendiculaire.
Donc la droite (BD) diagonale du carré, est perpendiculaire au segment [AC] et elle coupe de plus ce segment en son mileu : la droite (BD) n'est autre que la médiatrice de [AC]
Le triangle AKC est équilatéral par hypothèse. Donc KA=KC donc K appartient à la médiatrice de [AC]
Par conséquent, K,D,B sont bien alignés.
b/ Considère la rotation de centre C et d'angle  /3
/3
Tu as trois beaux triangles équilatéraux de couleur !
Quelle sont les images par cette rotation de :
K ---> ?
D ---> ?
B ---> ?
Propriété de la rotation : l'image d'une droite par une rotation est une droite.
La rotation conserve les distances, les angles etc... cf ton cours
B,D,K sont alignés donc tu peux en conclure...
Bonne soirée
Bonsoir, rudy_math, tout d'abord je tiens à vous remercier pour votre aide 
a) en ce qui concerne cette question, je me rends compte combien j'ai été stupide d'aller chercher des angles orientés, alors qu'en trois lignes c'est réglé.... merci 
b) par rotation d'angle pi/3
K a pour image A
D a pour image I
B a pour image J
Or la rotation conserve l'alignement donc A, I et J sont alignés

C'est bon ?


