Inscription / Connexion Nouveau Sujet
démonstration des formule d'addition et de duplication
On considére un repère orthonormé direct (O;I,J)
Soit C le cercle trigonométrique de centre O, et M et N les points du cercle C tel que:
vecteur OI scalaire vecteur OM (OI, OM) = b[2PI] et (OI,ON) = a où a et b désignent deux nombres réels quelconques.
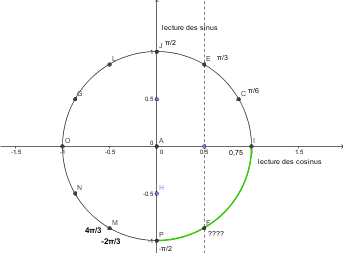
a) faire une figure (je bloque au moment ou il faut representer les vecteur scalaire a et b)
b) Exprimer en fonction de a et b les coordonnées des vecteurs OM et ON
Je n'y arrive pas du tout cette question b et jen et besoin pour continuer la suite, merci de bien vouloir me venir en aide car je suis désespéré
On considére un repère orthonormé direct (O;I,J)
Soit C le cercle trigonométrique de centre O, et M et N les points du cercle C tel que:
vecteur (OI, OM) = b[2PI] et (OI,ON) = a où a et b désignent deux nombres réels quelconques.
a) faire une figure (
b) Exprimer en fonction de a et b les coordonnées des vecteurs OM et ON
Je n'y arrive pas du tout cette question b et jen et besoin pour continuer la suite, merci de bien vouloir me venir en aide car je suis désespéré
en abscisse, tu lis le cosinus de l'angle
et en ordonnée tu lis le sinus de l'angle
regarde ton cours....
et pour ON c'est pareil alors mais tout depend de l'endroi ou je l'ai placé sur le cercle, si il et en bas a droite c'est N(cos a ; -sin a ) ?
ON pareil oui!
mais tout depend de l'endroi ou je l'ai placé sur le cercle, si il et en bas a droite c'est N(cos a ; -sin a ) ?
non !
c'est toujours (cosa, sina)
c'est la valeur de a qui dans le calcul, fera que le résultat calculé sera positif ou négatif
Merci beaucoup, cela va m'aider pour la suite, j'aurai peut etre encore besoin d'aide plutard. merci beaucoup
maintenant je n'arrive pas cette question, Montrern en utilisant la relation de Chasles pour les angle orientés, que l'angle des veteurs (OM,ON) = a-b [2PI] ??
On a jamais fait sa dans le cour, on je devais etre absent ce jour la.
(OM,ON) = (OM,OI)=(OI,ON) après j'en fait quoi ?


