Inscription / Connexion Nouveau Sujet
Démontrer qu'un triangle est équivalent au trapèze
Bonjour,
Voilà je ne comprends pas comment résoudre ce problème :
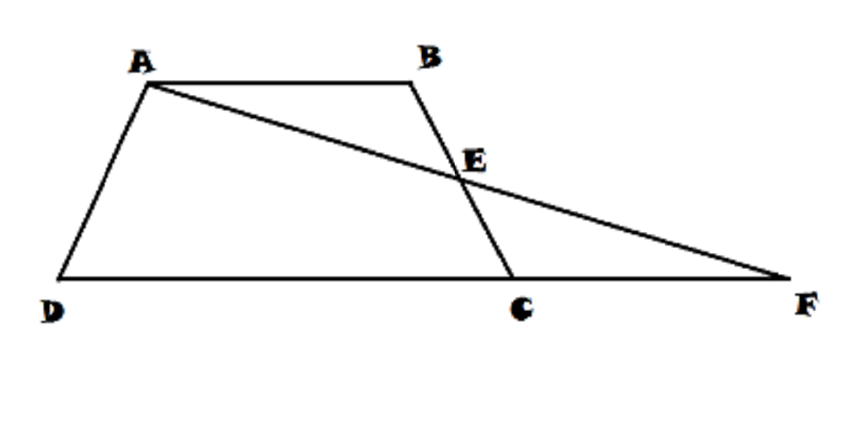
La droite qui joint un sommet A d'un trapèze au milieu de BC, coupe le prolongement de DC en F.
Démontrez que le triangle ADF est équivalent au trapèze.
Mon problème est le suivant je ne comprends pas comment résoudre cet exercice sachant que je n'est pas de mesure ni d'angle
Merci pour votre réponse 
les triangles ABE et FCE sont isométriques.
on est dans une configuration de Thalès en papillon.
donc leur aire sont égales.
D'accord pour Thalès.
Mais mon problème c'est que je n'est pas de mesure donc je ne peux prouver qu'ils sont isométrique ?
Dois-je le démontrer avec des lettres ?
(parce que personnellement ce n'est vraiment pas mon fort).
Pouvez-vous me donner des explications, qui pourrais m'éclairer ?
Merci !
Sans vous mentir je ne comprends pas grand chose quand il n'y a pas de nombres.
En plus mon prof aime quand tout celà est bien développer 
Oui, mais comment démontrer que CF = AB et que AE = EF
justement parce qu'on est dans une configuration de Thalès,
qu'on peut donc écrire la triple égalité du rapport des côtés
et que par hypothèse EB/EC = 1
Bonjour,
Donc la triple égalité des cotés est :
AE/EF = AB/CF = BE/EC
Mais comment démontrer que le triangle ADF est équivalent au trapéze ?
Merci.
démontrer que le triangle ADF est équivalent au trapéze.
Il doit s'agir, dans l'énoncé, de montrer que le triangle
ADF et le trapéze ont même superficie (aire égales).
s
Bonjour vu que nous sommes dans la configuration des cotés :
Pouvez-vous me dire si celà est correct ?
AE/EF = BE/EC = AB/CF
La point E étant le point d'attache pour ces deux triangles.
Hypothése :
Dans les triangles ABE et ECF :
Les points E,A,F d'une part et E,B,C d'autre part sont alignés.
Les droites (AB) et (CF) sont paralléles.
Le triangle ECF étant équivalent au triangle ABE, alors le triangle ADF est équivalent au trapéze ABCD.
MERCI !


