Bonjour, bizarre ce /45 ? il ne tourne pas plutôt de /4 ?
tu devrais d'abord simuler tout ça dans geogebra pour te faire une idée du résultat et aussi de ce qu'il faut calculer pour aboutir.

Non non je sais que c'est bizarre mais cet escargot tourne bien de /45!

Oui j'ai essayé sur géo gébra et je pense à un polygone à 90 cotés mais je ne parviens pas à reproduire la figure sur le logiciel

si c'est faisable, il faut utiliser le tableur :

ça sort au 36 ième pas. je peux te donner le détail des syntaxes à rentrer si tu as besoin.

Ce serait vraiment sympa de ta part, cela fait 2h que je cherche sur le logiciel..

Bonjour,

"le logiciel" n'est peut être pas forcément la panacée ... le salut vient peut être de la trigo et du calcul ...
et c'est peut être bien ce qui est attendu, ce calcul avec la trigo (et une simple calculette même pas programmable)

calcul du rayon du cercle circonscrit à un polygone connaissant le nombre de ses côtés et son angle au centre
calcul de l'angle au centre nécessaire pour atteindre le bord du champ
et donc nombre de fois l'angle de pi/45 pour avoir cet angle là.

il me semble que cela donne un polynôme 90 côtés
malou > ***lien supprimé***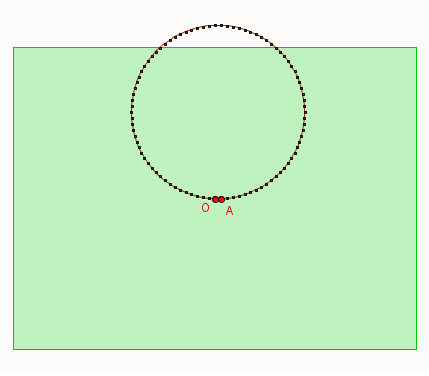

merci de mettre ton image sur le site la prochaine fois

Cette image ne vient pas de moi mais je sais qu'elle est bonne. Il faut que j'explique par le calcul mais je ne comprend pas ce que tu veux dire par "son angle au centre" et "de l'angle au centre nécessaire pour atteindre le bord du champ"

Donc on utilise la fenêtre tableur.
j'ai utilisé les nombres complexes car c'est plus simple (j'espère que tu sais ce que c'est ?).

dans la colonne A j'ai rentré 1;2;3; etc .... (tu tapes 1 et 2 et tu tires vers le bas)
la case B1 c'est le centre du jardinet donc z_0 = 2+1.5 i l'affixe du centre
dans la case B2 on rentre la formule de récurrence qui va nous permettre de calculer tous les points quand on va copier la formule vers le bas. on tape :
B1 + (6 / 100) e^(i (A2 - 1) pi / 45)
qui veut dire que pour avoir le point suivant on part du précédent et on rajoute un nombre complexe de 6/100 de module et d'angle (n-1)pi/45
Quand on tire la formule vers le bas, ça calcule tous les points par la formule de récurrence

les points obtenus sont automatiquement implanté dans la fenêtre graphique, on a rien besoin de faire. j'ai rentré un rectangle de 4 de long sur 3 de haut tout au début.

il n'y a plus qu'à regarder quand est-ce qu'un point déborde du rectangle.

Bonsoir,
Je te suggère de le faire avec Excel.
On part x₀=0=y₀
x₁=0.06    y₁=0
x₂=x₁+0.06*cos(/45)   y₂=y₁+0.06*sin(/45)
.
.
.
x_n+1=x_n+0.06*cos(n/45)
y_n+1=y_n+0.06*sin(n/45)

Reste à savoir si Nord-Sud on a les 3 mètres ou les 4 mètres...moi, je trouve qu'au bout de 36min il est à plus de 1.5m vers le nord...
Sauf erreur !
J'arrive après le combat, mais je poste quand-même !

je veux dire faire une figure "de principe" et pas avec des bidules illisibles, pour raisonner avec de la trigo



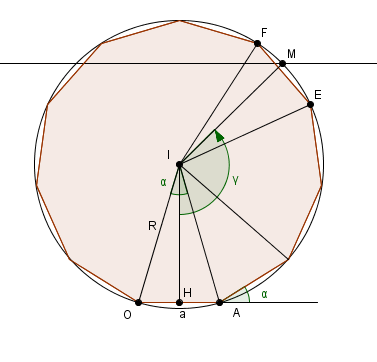
l'angle au centre du polygone c'est (numériquement on sait que c'est pi/45)
on connait OA = a = 6cm
on en déduit R par la trigo
et même au besoin IH (donnant la position du centre)

l'angle au centre à considérer pour atteindre le bord du champ c'est (ou à peu près, vu que M sera dans le secteur "entre" E et F que l'on prenne l'intersection du cercle avec le bord du champ ou l'intersection du segment EF avec le bord du champ ça reviendra au même, et que l'on cherche l'angle OIM ou l'angle HIM, c'est kif-kif vu que la différence entre les deux c'est pi/90 connue, on choisira celui qui donne le calcul le plus simple.


évidemment si l'exercice est conçu non pas comme un exercice de trigo mais comme un exercice de programmation (de tableur) ...
pas la peine de se fouler et la suite des "altitudes" de l'escargot, consciencieusement programmée dans un tableur donne le résultat directement sans effort.

moi je suis d'accord, mathafou, il faut démontrer par de la trigo. la simulation c'était juste pour se faire une idée de la trajectoire parcourue.

(j'aime bien ton " directement sans effort" alors que les gens peinent affreusement dans les algorithmes ou sur les tableurs , tout le monde n'est pas mathafou)

oui c'est "un peu" exagéré le "directement sans effort" !!
et puis de toute façon il y a tout de même un bon bout de trigo dans l'algorithme / formules à saisir...