Bonjour,
je suis totalement bloquée par cette exercice pour mon DM. Pourriez vous m'aidez s'il vous plait.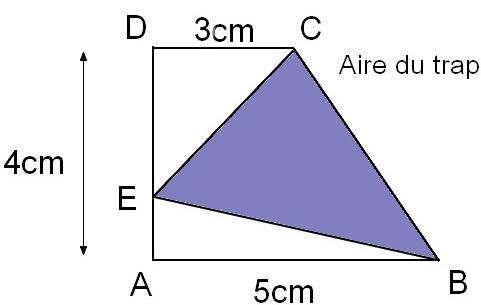


_{* Océane > Andalousi si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum. *}

Bonsoir Andalousi

Et de quel exercice s'agit-il ?

*** message déplacé ***

Bonsoir,

Commence par noter avec x la longueur AE. Que devient la condition a) si tout mets cela en équation ?

J'ai eu un petit beug avec mon image donc je l'ai reposté je te donne le lien.
Merci Elisabeth67 de te pencher sur mon problème.


https://www.ilemaths.net/sujet-deplacement-d-un-point-pour-changer-l-aire-d-un-916-et-trapez-454366.html

*** message déplacé ***

x la longueur AE
pour moi il faudrait que je trouve la longueur EC CB EB mais comment je ne sais pas.

Tu te compliques si tu cherches EC,CB,EB !

Pense aux jolis triangles rectangles de la figure et calcule leurs aires.
Quelle part de l'aire du trapèze représente la somme de leurs aires ? (et tu auras ton équation !!)

Le conseil qu'on t'a donnée est bon ;on appelle AE = x

Déjà , calcule l'aire du trapèze ABCD

Puis l'aire du triangle rectangle AEB (5*x/2), puis celle du triangle rectangle DEC ( DE = 4-x )

L'aire de BEC s'obtiendra en faisant :
aire du trapèze ABCD - aire du triangle rectangle AEB - aire du triangle rectangle AEB

*** message déplacé ***

Dac j'ai deja chercher l'aire du trapèze qui vaut 16cm²
aire de ABE = (3*x)/2
avec x=3
(3*3)/2= 4.5cm²
aire de EAB= ((4-3)*5)/2
(1*5)/2=2.4

Il ne faut pas donner de valeur à x ; reste dans le cas général

AEB : (5*x/2) = 5x/2

ECD : DA = (4-x) DC = 3   donc aire de DEC = ......

Ah oui
ECD : DA = ((4-x)*5/2
DC = 3
et après ... ? Je fais comment pour les 40%

Additionne les 2 aires à soustraire à celle du trapèze
5x/2 + 3(4-x)/2

Ce total doit être égal pour la 1ère question à la moitié de l'aire du trapèze , c'est à dire à 8
Donc on résout
5x/2 + 3(4-x)/2 = 8


Pour la 2ème question , pour que BEC ait 40% de l'aire du trapèze , il faut donc que la somme précédente soit égale à 60% de 16 , soit 9,6

On résout 5x/2 + 3(4-x)/2 = 9,6