Salut,

Sur , .

Il est clair que f est dérivable sur puisqu'elle est le produit de deux fonction définies et dérivables sur (à savoir et ).

à+

salut
pour x >= 0 on a :
f(x)=x/(x+1) fonction derivable sur ]0,+oo[ (car compose et produit de fonction derivable sur ]0,+oo[)

f'(x)=1/(x+1)²

reste a voir la derivabilite de f en 0.
lim f(h)/h = lim 1/(h+1) = 1
h->0+
lim f(h)/h= lim 1/(1-h) = 1
h->0-
donc f derivable en 0.

En image

Philoux

Merci cinnamon et Minotaure.

C'était tout bête en fait, mais merci quand même, j'y avais pas pensé.

Merci aussi philoux.

De plus, j'aurais une autre question à laquelle je ne sais pas répondre svp.

La voici:
On considère un réel y de l'intervalle ]-1;1[, déterminer par le calcul l'unique antécédent x de y par f, exprimer simplement x en fonction de y.

Re pierrette

Tu dois trouver x = y/(1-|y|) avec -1<y<1

Je dois quitter l'île et te laisse aux mains des autres mathîliens,

Bon courage,

Philoux

Merci encore philoux, mais je ne comprends pas très bien comment tu arrives au résultat. Quelqu'un pourrait-il m'expliquer?

Ya personne qui peut m'aider svp, pour que je puisse faire la suite?

Personne ne sait répondre à cette question svp?

Pierrette, tu peux aussi essayer d'y arriver seule.

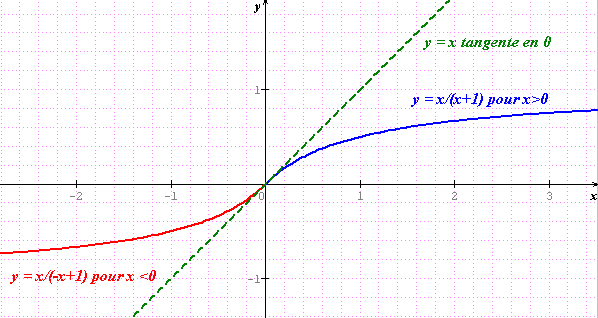
Etudions les variations de .

Pour x positif,
est strictement décroissante, est strictement croissante, donc f est strictement croissante de vers (asymptote horizontale en )

Pour x négatif,
est strictement croissante, donc f est strictement croissante de vers (asymptote horizontale en )

Au total, f est (une bijection) strictement croissante de vers

Cf. représentations graphiques ci-dessus.

On en déduit que tout y de ]-1;1[ a un unique antécédent unique x par f.

Si , on sait que et :


(avec y>0)

Si , on sait que et :


(avec y<0)

Au total :


Nicolas

Merci encore Nicolas.
Au revoir!

Voila, juste une petite question pour finir mo devoir:

Soit les fonctions f et g telles que:
f(x)=x/(!x!+1)
g(x)=x/(1-!x!)
( Les points d'exclaation remplacent les valeurs absolues )

Pour tout x de ]-1;1[, calculer f[rond]g(x). Montrer que le symétrique du point M(x;y) par la symétrie d'axe y=x est le point N(y;x). En déduire que pour tout x de ]-1;1[ le symétrique de tout point M de (Cg) d'abscisse x est sur (Cf). Qu'en déduit-on pour les 2 courbes?

*** message déplacé ***

Salut pierrette

Tiens, tiens : la suite d'hier...

fog(x) = f (g(x)) = f ( x/(1-|x| ) = ...

Tu continues ?

Philoux

*** message déplacé ***

J'ai déjà continué, mais j'arrive à un résultat que je ne sais pas simplifier!
fog(x)= [x/(1-!x!)]/[!x/(1-!x!)!+1]

( les points d'exclamation remplacent toujours les valeurs absolues!)
Pouvez-vous m'aider svp?

*** message déplacé ***

Bonjour,

Décidemment les règles du forum t'importent vraiment peu...

Dernier avertissement :

[faq]multi[/faq]

Merci de respecter les règle desormais
A+

J'ai déjà continué, et J'arrive a un résultat bizarre que j'arrive pas à simplifier!
fog(x)= [x/(1-!x!)]/[!x/(1-!x!)!+1]
Les points d'exclamation remplacent toujours les valeurs absolues!
Pouvez-vous m'aider svp?

Bonjour jérome,

si je puis me permettre, ce n'est pas vraiment du multi-post puisque c'est la suite d'un post initialisé hier.

Philoux

pierrette

Toujours la même méthode : définis des intervalles dans lesquels tu peux éliminer les barres de valeurs absolues.

(_{A ce propos, pour les faire, ces barres, utilises "Alt Gr" 6})

Tu essaies ?

Philoux

Salut philoux

Je pense qu'il aurait pu poster dans le meme topic car le sujet est identique...

Je vois ça comme ceci après j'ai peut-etre tord je me suis pas penché sur son problème en détail non plus...

Cordialement,
Jérôme

PAs de souci,

Je pense que pierrette a désormais compris

Philoux

Ok, merci philoux. J'ai trouvé:
fog(x)=x pour x appartient à ]-1;0]
fog(x)=x pour x appartient à [0;1[
Est-ce cela?

Sinon, pourriez-vous m'aider pour la suite de la qustion ( symétrique ) svp?

Tu essaies cette question :

Montrer que le symétrique du point M(x;y) par la symétrie d'axe y=x est le point N(y;x).
Philoux

J'ai déjà essayé mais je ne trouvepas. Pourrais-tu me donner un conseil, un indice stp?

Si M et N sont symétriques

Exprimes les coordonnées du milieu I de M et N

Et regardes où se trouve I

Conclues

Philoux

Ok, merci, et qu'est-ce que j'en déduit stp?

Cherches un peu...

N'oublies pas aussi de montrer que MN est à angle droit avec y=x

Philoux

Et comment je montre que MN est à angle droit avec y=x?

J'ai trouvé!

Mais une question subsiste: comment fait-on pour en déduire la question suivante?
Pourriez-vous m'aider?
Merci d'avance

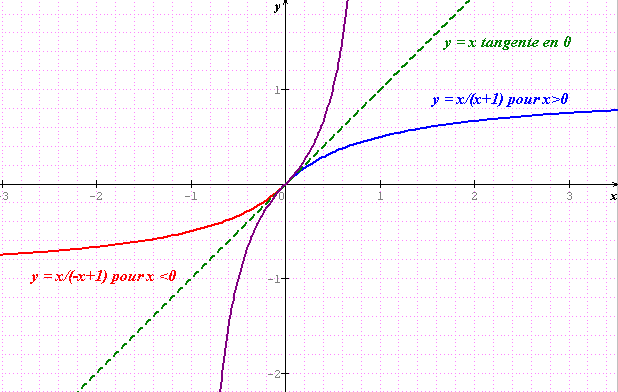
Regardes les courbes de 20:04 hier

et au vu de tes démonstrations sur :

1) fog(x)=x

2) M symétrique de N par rapport à N

Que conclus-tu sur les positions relatives des courbes en terme de symétrie ?

Philoux

Je ne vois pas comment me servir du fog(x)=x.
Pouvez- vous m'expliquer?

Personne ne peut m'aider svp?

Vrément personne qui peut m'aider svp?

pierrette, il va falloir que tu deviennes un peu plus autonome...

et

Pour tout x de ]-1;1[, calculer fog(x).

Première méthode

On a vu le 3/9 à 5h44 que est la fonction réciproque de . (Regarde bien, c'est la même expression). Donc et . Terminé.

Seconde méthode

Tu peux aussi calculer si tu veux, mais c'est inutile après les questions précédentes.

Or, sur ]-1;1[, , donc
Donc :

On multiplie numérateur et dénominateur par :

Donc, il n'était même pas besoin de distinguer selon le signe de x !

Montrer que le symétrique du point M(x;y) par la symétrie d'axe y=x est le point N(y;x).

Soit I le milieu de [MN]. Il nous faut montrer que :
(i) I est sur la droite y=x
(ii) (MN) est perpendiculaire à la droite y=x
I a pour coordonnées donc (i) est évident.
a pour coordonnées (y-x;x-y)
La droite y=x admet comme vecteur directeur de coordonnées (1;1)
d'où

En déduire que pour tout x de ]-1;1[ le symétrique de tout point M de (Cg) d'abscisse x est sur (Cf).

Soit (x,g(x)) un point de (Gg).
Son symétrique est (g(x),x).
Est-il sur (Cf) ?
Pour le savoir, regardons si f(g(x))=x
C'est bien le cas, d'après les questions antérieures.
Donc le symétrique est sur (Cf).

Qu'en déduit-on pour les 2 courbes?

Les 2 courbes sont symétriques par rapport à la droite y=x.

Merci Nicolas_75. Mais j'avais déjà trouvé les réponses aux 2 premières questions. Mais merci quand même, ca m'a permis de vérifier mes calculs.

Je me permets de répéter que, pour montrer que fog(x)=x, il n'y a pas de calcul à faire. Regarde ma "première méthode" : elle utilise la question précédente. C'est cela que ton professeur attend, à mon avis.

Merci encore. Une autre petite question ( je ne suis ps fort avec les lettres ):

Soit la fonction f telle que:
f(x)=x/(|x|+1)

On considère un réel y de l'intervalle ]-1;1[, déterminer par le calcul l'unique antécédent x de y par f, exprimer simplement x en fonction de y.
Cette question a déjà été répondue, mais dans le mauvais sens. Il faudrait en effet d'abord trouver la formule générale, puis faire la suite de la question ( et pas l'inverse ).

Merci d'avance.

J'ai déjà répondu à cette question le 03/09/2005 à 05:44, et dans le bon sens !

Mais non, puisque tu as déjà étudié x en fonction du signe de y avant de trouvez la formule générale. C'est l'inverse qu'il faut faire. D'abord la formule générale, puis x en fonction du signe de y.
Tu n'as donc pas répondu dans le bon sens.

Quelqu'un pourrait-il m'aider?

"Quelqu'un pourrait-il m'aider?"
je comprends que tu veux dire : "quelqu'un d'autre" ?

Pierrette, là, tu dépasses les bornes.
J'ai passé beaucoup de temps à t'aider, et tu ne m'écoutes pas.

On considère un réel y de l'intervalle ]-1;1[, déterminer par le calcul l'unique antécédent x de y par f, exprimer simplement x en fonction de y.

On cherche x tel que y=f(x).

Dans mon message du 03/09/2005 à 05:44 :
1) je montre d'abord que x est unique (puisque f est (une bijection) strictement croissante )
2) puis j'exprime x en fonction de y

Nicolas

Lire :
1) je montre d'abord que x existe et est unique (puisque f est (une bijection) strictement croissante)

Mais non, ya pas besoin de montrer que x est unique, puisqu'on le dit. I faut d'abord trouver la formule générale, puis donner x en fonction de y.

Attends, je t'aide: il faut trouver ton résultat précédent avant de faire ta démonstration que tu as mis avant.
En gros, il ne faut pas s'aider du signe de y.

PS: je ne sais pas ce qu'est une bijection!!
Oh puis zut à la fin, arrête de me parler de ca.

OK, pierrette, j'arrête de t'en parler.
J'espère que tu as bien mesuré ce que tu viens d'écrire.

oui pourquoi?

Je ne t'insulte pas, mais tu me parles de bijection. Peux-tu m'expliquer au moins le terme stp?

Oublie le terme de bijection.

J'ai étudié la fonction, et en ai déduit que f est strictement croissante de sur
Donc chaque y de ]-1;+1[ admet un antécédent x unique.
Pour moi, il fallait le démontrer
Toi, tu dis que cette information était déjà dans l'énoncé, et qu'il ne servait à rien de le démontrer. OK. Oublie aussi ce paragraphe.

Après, il faut exprimer x en fonction de y.
Or la seule information dont tu disposes est :
y=f(x), c'est-à-dire

Là, pour continuer, il faut bien faire une hypothèse sur le signe de x.
Or, on ne connait pas encore x, on ne connait que y.
Néanmoins, après avoir étudié la fonction, on sait que x et y sont positifs en même temps ou négatifs en même temps (regarde les graphes ci-dessus)

Prenons le cas y positif.
Alors x est positif aussi. On remplace |x| par x
Et on résoud l'équation.
On trouve x en fonction de y.

Prenons ensuite le cas y négatif.
Alors x est négatif aussi. On remplace |x| par -x
Et on résoud l'équation.
On trouve x en fonction de y.

A la fin, les 2 expressions de x en fonction de y (l'une pour y positif et l'autre pour y négatif) se fondent en une seule en introduisant |y|

Pour moi, c'est la seule façon rigoureuse (et logique) de faire.

Tu peux faire autrement si tu veux, mais STP, ne dis pas que j'écris des bêtises.

Ca va ?

Nicolas

ok, merci encore. C'est pas grave, je vais faire comme ca s'il n'y a aucune autre solution!
Merci encore

Fais comme tu veux, Pierrette.
Je vais quitter l'Île, et te souhaite une bonne soirée.

Nicolas