Inscription / Connexion Nouveau Sujet
Dérivation
Dans une clinique vétérinaire, pour soigner un petit chaton malade, on lui administre un médicament par intraveineuse.
On note f(t) la quantité de produit (en milligrammes) présente dans le sang t heures après l'intraveineuse, t appartenant à l'intervalle [0; 24].
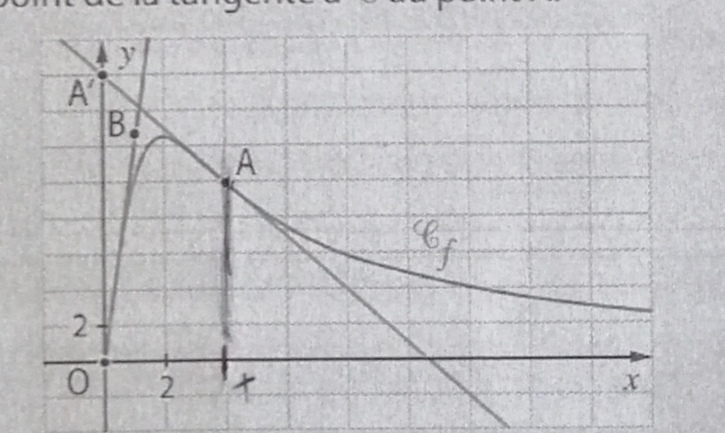
Le point A(4; 10) est un point de C. Le point B(1;12,5) est
un point de la tangente à C au point O et le point A' (0; 16)
est un point de la tangente à C au point A.
1. Déterminer graphiquement la vitesse de diffusion du
produit à t= 4.
J'ai trouver 10 mais je ne sais aps en quelle unité je dois mettre.
2.On admet que pour tout i appartenant à [0; 24]:
f(t) = 50t/t2+4
a. Retrouver par le calcul la réponse apportée à la question 1.
Ça fait 200/20 donc 10.
b. Calculer la vitesse initiale de diffusion du produit.
bonjour
J'ai trouver 10 mais je ne sais aps en quelle unité je dois mettre.
relis ton énoncé, on dit dans quelle unité on travaille
une vitesse de diffusion....n'y aurait-il pas un lien avec une dérivée ? un nombre dérivé ? une tangente ?
Bonjour,
1. En d'autres termes, on cherche ici la valeur de la dérivée de en
. Cela revient à déterminer la pente de la tangente à
au point
. Comme
et
sont deux points appartenant à cette tangente, tu peux facilement trouver la valeur de sa pente. Montre moi le détail de ton calcul, parce que je ne trouve pas 10 !
On calcule ici la variation de produit présent dans le sang (en mg) par rapport au temps t (en h). L'unité de ton résultat sera donc en mg/h. (D'ailleurs, dans le calcul de la pente de la tangente, on divise bien des milligrammes par des heures !).
2. Peux-tu réécrire correctement l'expression de ? Elle ne semble en effet pas correcte (attention aux parenthèses).
2.a. Il s'agit ici de dériver la fonction et de donner la valeur de
/
2.b. Idem que question 1. en utilisant la tangente à l'origine .
Peux-tu nous montrer ce que tu as fais pour obtenir 10 mg/h, parce qu'il ne s'agit pas de la bonne réponse ?
Relis bien l'énoncé et ma première réponse. On s'intéresse ici à la variation de la quantité de produit dans de temps, c'est-à-dire à la valeur de la dérivée de .
Je suppose que par r(h) tu veux dire le taux d'accroissement de f en . Revenir à la définition de la dérivée avec le taux d'accroissement, ça sera plus compliqué. Détermine directement l'expression de f' et calcule ensuite f'(4).
Non le numérateur ici n'est pas une constante, tu ne peux pas directement utiliser la règle de dérivation de 1/u. Utilise la règle de dérivation pour u/v.
Oui ! Alors combien vaut la vitesse de diffusion du produit à t = 4h ?
Et vérifie maintenant que tu trouves la même chose graphiquement pour la question 1.
Ce qui t'inquiète c'est le signe négatif ? En observant la courbe, on voit que f est décroissante en t = 4h, c'est alors normal que la valeur de sa dérivée soit négative. Comment peut-on interpréter la courbe de f:
· de t = 0h à t = 2h : la quantité de produit dans le sang augmente (la dérivée est donc positive). C'est la phase de diffusion vers le sang, durant laquelle le médicament ce répand dans tout le système sanguin du chat.
· à t = 2h : la quantité de produit dans le sang est maximale (la dérivée est donc nulle). A ce moment là le médicament est réparti dans tout le sang. A partir de là, le médicament ne se diffuse plus dans le sang.
· à partir de t = 2h, la quantité de produit dans le sang diminue (la dérivée est donc négative). Si la quantité de médicament diminue, c'est que le médicament est "consommé" par les organes. La diffusion ne se fait plus vers le sang mais en dehors du sang et vers les organes (d'où le signe négatif : le produit part du sang vers les organes)
Dans la question 1 on cherche aussi à évaluer f'(4). Le problème c'est que l'expression de f n'est pas donnée. Il faut alors se rappeler de la définition de la dérivée en un point : f'(4) c'est justement la valeur de la pente de la tangente de en t=4.
Est-ce que t'as réussi à trouver la pente de cette tangente ?
Oui tu as raison, ici on peut utiliser les carreaux du graphique ; mais parce que la même échelle est utilisée pour les deux axes (1 carreau = 2 unité pour les deux axes).
Mais pour la question 2.b) on ne pourra pas utiliser les carreaux ; il faut utiliser les coordonnées des points et
pour trouver la pente de la tangente en
.
ah oui du coup on regarde ce qui se passe pour un carreaux ce qui se passe (coeff directeur) et on trouve -1.5


